Existential Graphs

Existential Graphs (die deutschen Übersetzungen „existenzielle Graphen“ und „Existenzgraphen“ sind nicht sehr gebräuchlich) sind ein logisches System des US-amerikanischen Logikers und Philosophen Charles Sanders Peirce. Sie umfassen sowohl eine eigene graphische Schreibweise (Notation) für logische Aussagen als auch einen logischen Kalkül, d. h. (im Wesentlichen) ein formales System von Schlussregeln, mit denen bestehende Aussagen so umgeformt werden können, dass daraus neue Aussagen entstehen, die aus ersteren folgen.

Einleitung

Peirce empfand die algebraische Schreibweise (d. h. Formelschreibweise) der Logik, vor allem die der zu seinen Lebzeiten noch sehr neuen, von ihm selbst wesentlich mitentwickelten[1] Prädikatenlogik philosophisch als unbefriedigend, weil den Formelzeichen ihre Bedeutung durch bloße Konvention zukomme. Im Gegensatz dazu strebte er eine Schreibweise an, bei der die Zeichen ihre Bedeutung buchstäblich in sich tragen[2] – in der Begrifflichkeit seiner Zeichentheorie: ein System ikonischer Zeichen, die den bezeichneten Gegenständen und Relationen ähneln oder gleichen.[3]

So war die Entwicklung eines ikonischen, graphischen und – wie er beabsichtigte – damit intuitiven und leicht erlernbaren logischen Systems ein Projekt, das Peirce zeitlebens beschäftigte. Nach mindestens einem abgebrochenen Ansatz – den „Entitative Graphs“ – entstand schließlich von 1896 an das geschlossene System der Existential Graphs. Obwohl von ihrem Schöpfer als klar überlegenes und intuitiveres System betrachtet, waren sie als Schreibweise und als Kalkül ohne größeren Einfluss auf die Geschichte der Logik; zurückgeführt wird das einerseits darauf, dass Peirce zu diesem Thema nur wenig publizierte und die veröffentlichten Texte nicht sehr verständlich geschrieben seien;[4] und andererseits darauf, dass die lineare Formelschreibweise in der Hand von Fachleuten das weniger aufwändig handhabbare Werkzeug sei.[5] So wurden die Existential Graphs nur wenig beachtet[6] oder als unhandliche Schreibweise angesehen.[7]

Zu besserem Verständnis führten ab 1963 Arbeiten von Don D. Roberts und J. Jay Zeman, in denen Peirce’ graphische Systeme systematisch untersucht und dargestellt wurden. Eine praktische Rolle spielt heute allerdings nur eine moderne Anwendung, die 1976 von John F. Sowa eingeführten Begriffsgraphen, die in der Informatik zur Wissensrepräsentation verwendet werden. Als Forschungsgegenstand treten die Existential Graphs im Zusammenhang mit einem wachsenden Interesse an graphischer Logik wieder vermehrt in Erscheinung,[8] was sich auch in Versuchen äußert, die von Peirce angegebenen Schlussregeln durch intuitivere zu ersetzen.[9]

Das Gesamtsystem der Existential Graphs setzt sich aus drei aufeinander aufbauenden Teilsystemen zusammen, den Alphagraphen, den Betagraphen und den Gammagraphen. Die Alphagraphen sind ein rein aussagenlogisches System. Auf sie aufbauend entstehen als echte Erweiterung die Betagraphen, ein prädikatenlogisches System der ersten Stufe. Die bis heute nicht vollständig erforschten und von Peirce nicht vollendeten Gammagraphen werden als Weiterentwicklung der Alpha- und Betagraphen verstanden. Bei geeigneter Interpretation decken die Gammagraphen Prädikatenlogik höherer Stufe sowie Modallogik ab. Noch 1903 begann Peirce mit einem neuen Ansatz, den „Tinctured Existential Graphs,“ mit denen er die bisherigen Systeme der Alpha-, Beta- und Gammagraphen ablösen und deren Ausdrucksstärke und Leistungsfähigkeit in einem einzigen neuen System vereinen wollte. Wie die Gammagraphen blieben die „Tinctured Existential Graphs“ unvollendet.

Als Kalküle sind die Alpha- und Betagraphen sowohl korrekt (d. h., alle als Alpha- bzw. Betagraphen herleitbaren Ausdrücke sind aussagen- bzw. prädikatenlogisch semantisch gültig) als auch vollständig (d. h., alle aussagen- bzw. prädikatenlogisch semantisch gültigen Ausdrücke sind als Alpha- bzw. Betagraphen herleitbar).[10]

Die Wahl der Bezeichnung „Existential Graphs“ begründet Peirce damit, dass der einfachste sinnvolle und wohlgeformte Betagraph eine Existenzaussage trifft.[11] Peirce verwendet diese Bezeichnung erstmals Ende 1897;[12] zuvor spricht er von „positive logical graphs“ oder einfach von seinem System logischer Diagramme.

Der vorliegende Artikel behandelt die Alpha- und Betagraphen als den vollendeten und am besten erforschten Teil von Peirce’ System. Darüber hinausgehende Informationen bieten die in der Literaturliste genannten Werke.

Alphagraphen

Notation der Alphagraphen

Alphagraphen

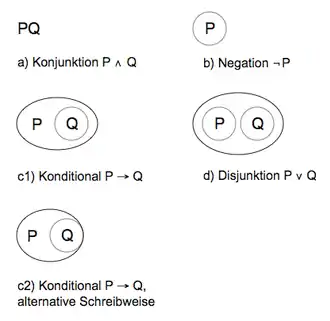
Atomare Aussagen, d. h. solche Aussagen, die ihrerseits nicht aus anderen Aussagen zusammengesetzt sind, werden – wie in der Aussagenlogik üblich – durch Buchstaben ausgedrückt; zum Beispiel kann die atomare Aussage „Es regnet“ durch den Buchstaben „P“ ausgedrückt werden. Die Konjunktion mehrerer – atomarer oder nicht atomarer – Aussagen wird durch ihr Nebeneinanderschreiben ausgedrückt. Um zu sagen, dass zwei Aussagen P und Q wahr sind, schreibt man daher „PQ“.

Neben der Konjunktion umfasst das System die Negation. Sie wird ausgedrückt, indem der zu verneinende Ausdruck – egal ob einfach oder zusammengesetzt – von einem geschlossenen Linienzug umgeben wird, sozusagen „eingeringelt“ wird. Spezielle Anforderungen an die Gestalt des Linienzugs werden keine gemacht, es ist aber gebräuchlich, einen Kreis oder ein Oval zu verwenden. Den geschlossenen Linienzug, der eine Aussage verneint, nennt Peirce den Cut (wörtlich: Schnitt). Bildlicher Hintergrund des Cuts ist, dass auf dem Blatt Papier, auf dem geschrieben wird – dem sheet of assertion, Annahmeblatt –, die als wahr angenommenen Aussagen niedergeschrieben werden. Falsche Aussagen müssen vom Bereich der wahren Aussagen ausgeschlossen, abgegrenzt, „abgeschnitten“ werden, und ebendiese Funktion übernimmt der Cut.

Um ein Konditional auszudrücken, d. h., um zu sagen, dass eine Aussage P eine hinreichende Bedingung für eine Aussage Q ist, wird eine Schreibweise gewählt, die im Englischen als „P scrolls Q“, „P ringelt Q ein“, bezeichnet wird: Die Aussage Q, also der bedingte Satz, steht innerhalb eines eigenen Cuts gemeinsam mit seiner Bedingung, der Aussage P, in einem zweiten, äußeren Cut (siehe Abbildung, Punkt c1 und c2). Diese Schreibweise ist im logischen System der Existential Graphs atomar eingeführt, aber im Wissen, dass es sich bei dem Cut um die Negation und beim Nebeneinanderschreiben um die Konjunktion handelt, leicht mit den Wahrheitsbedingungen dieser beiden Verknüpfungen in Deckung zu bringen: Das Konditional, P→Q, ist äquivalent mit der Negation ¬(P ∧ ¬Q), und genau das ist die Aussage des „P scrolls Q“, die genau den Fall des wahren P und falschen Q vom sheet of assertion abgrenzt, „herausschneidet“.

Die Disjunktion wird ausgedrückt, indem die beiden Disjunkte – jeweils für sich in einzelne Cuts gesetzt – nebeneinander geschrieben und mit einem zusätzlichen äußeren Cut versehen werden. Man sieht leicht, dass diese Schreibweise in moderner Notation die Aussage ¬(¬P∧¬Q) darstellt, eine Aussage, die mit P∨Q äquivalent ist. Bildlicher Hintergrund ist wieder, dass die Disjunktion den Fall vom sheet of assertion ausschließt, dass sowohl P als auch Q falsch sind.

Mit den beiden Verknüpfungen der Alphagraphen, der Verneinung (dem Cut) und der Und-Verknüpfung (Aufschreiben mehrerer Aussagen auf dem Annahmeblatt) lassen sich – wie für das Konditional und die Disjunktion beispielhaft gezeigt wurde – alle anderen Verknüpfungen der zweiwertigen Aussagenlogik darstellen (siehe funktionale Vollständigkeit von Junktoren). Alphagraphen sind damit eine vollwertige Schreibweise für die Aussagenlogik.

Wenn Aussagen in der Schreibweise der Alphagraphen von elektronischen Rechenanlagen verarbeitet oder einfach mit Textverarbeitungssystemen bzw. früher Schreibmaschinen wiedergegeben werden sollen, behilft man sich oft damit, die Cuts durch Klammerungen auszudrücken. Statt eines geschlossenen Linienzugs um den Satz P zu zeichnen, schreibt man in diesem Fall (P). Das Konditional, „P scrolls Q“, wird in dieser Schreibweise zu (P(Q)). Aus typographischen Gründen wird auch in diesem Artikel so vorgegangen.

Schlussregeln der Alphagraphen

Um die Regeln formulieren zu können, ist es zunächst erforderlich, das Konzept der Ebene einer Aussage (in der Literatur: „proposition level“) zu definieren. Die Ebene einer – elementaren oder zusammengesetzten – Aussage ist definiert als die Anzahl der Cuts, von denen diese Aussage direkt oder indirekt umschlossen ist. Zum Beispiel ist im Ausdruck (P(Q)) die Ebene von P und jene von (Q) 1, weil sowohl P als auch (Q) nur Teil des äußeren Cuts sind. Die Ebene von Q hingegen ist 2, weil Q nicht nur unmittelbar von einem Cut umgeben ist, sondern dieser wiederum Teil des äußeren Cuts ist.

Nach dieser Vorbemerkung lassen sich die Schlussregeln wie folgt angeben:[13]

Annahme: Die Regel der Annahme erlaubt es, eine beliebige Aussage als Prämisse aufzuschreiben und von ihr ausgehend Folgerungen zu ziehen. Möchte man ein Argument herleiten, das mehr als eine Prämisse umfasst, dann schreibt man die Prämissen nebeneinander – Nebeneinanderschreiben bedeutet ja nichts anderes, als jeden der so kombinierten Sätze anzunehmen.
R1 – Löschregel („Rule of Erasure“): Jede Aussage, die auf geradzahliger Ebene auftritt, darf ersatzlos gestrichen werden. Mit dieser Regel kann man zum Beispiel von (P(Q)) durch Löschung von Q auf (P()) schließen, weil Q auf Ebene 2 liegt und 2 eine gerade Zahl ist. Nicht gelöscht werden dürfte in diesem Beispiel P, weil P auf Ebene 1 liegt und 1 eine ungerade Zahl ist.
R2 – Einfügungsregel („Rule of Insertion“): Auf ungeradzahliger Ebene darf jede beliebige Aussage eingefügt werden. Zum Beispiel ist es zulässig, mit dieser Regel aus (P(Q)) auf (PR(Q)) zu schließen: Die eingefügte Aussage, R, kommt auf Ebene 1 zu stehen, und 1 ist eine ungerade Zahl.
R3 – Wiederholungsregel („Rule of Iteration“): Jede Aussage, die Teil einer zusammengesetzten Aussage ist, darf auf derselben Ebene oder auf tieferer Ebene wiederholt werden, jedoch nicht innerhalb ihrer selbst. Nach R3 darf zum Beispiel aus (P(Q)) durch Wiederholung von P auf derselben Ebene auf (P(Q)P) oder durch Wiederholung von P auf tieferer Ebene auf (P(QP)) geschlossen werden. Ebenso darf aus derselben Aussage durch Wiederholung von (Q) auf (P(Q)(Q)) geschlossen werden. Nicht zulässig wäre es, (Q) innerhalb seiner selbst zu wiederholen und so auf (P(Q(Q))) zu schließen – diese theoretische Möglichkeit wird durch die Zusatzbedingung, dass die Wiederholung einer Aussage nicht innerhalb ihrer selbst erfolgen darf, ausgeschlossen.
R4 – Aufhebung der Wiederholung („Rule of Deiteration“): Wenn eine Aussage X formal von einer Gestalt ist, dass sie aus einer Aussage Y durch Anwendung von R3, der Wiederholungsregel, entstanden sein könnte, dann darf mittels R4 von X auf Y geschlossen werden; es ist dazu nicht erforderlich, dass X tatsächlich durch eine Anwendung von R3 entstanden ist. Zum Beispiel darf mit R4 von (P(Q)(Q)) auf (P(Q)) geschlossen werden, weil mittels R3 von (P(Q)) auf (P(Q)(Q)) geschlossen werden dürfte.
R5 – Regel des doppelten Cut („Rule of the Double Cut“): Doppelte Cuts dürfen nach Belieben eingefügt und gestrichen werden, sowohl um bestehende Aussagen herum als auch für sich alleine. Zum Beispiel darf nach R5 von PQ auf P((Q)), auf ((P))Q und auch auf ((PQ)) geschlossen werden. Ebenso darf aber von PQ auf PQ(()) oder auf P(())Q geschlossen werden.

Beispiel

Es soll aus $P\rightarrow Q$ und $Q\rightarrow R$ die Aussage $P\rightarrow R$ abgeleitet werden (Kettenschluss). Dazu beginnt man mit den Annahmen (P(Q)) und (Q(R)) und leitet schrittweise die Aussage (P(R)) her:

(P(Q))(Q(R))	$\longrightarrow$	(P(Q(Q(R))))(Q(R))	(R3)
(P(Q(Q(R))))(Q(R))	$\longrightarrow$	(P(Q(Q(R))))	(R1)
(P(Q(Q(R))))	$\longrightarrow$	(P(Q((R))))	(R4)
(P(Q((R))))	$\longrightarrow$	(P(QR))	(R5)
(P(QR))	$\longrightarrow$	(P(R))	(R1)

Betagraphen

Die Betagraphen sind das prädikatenlogische System der Existential Graphs. Sie erweitern das System der Alphagraphen um das Sprachmittel der Identitätslinie („line of identity“) und verallgemeinern die bereits bestehenden Schlussregeln.

Die atomaren Ausdrücke sind bei den Betagraphen nicht mehr Aussagebuchstaben (P, Q, R,…) bzw. Aussagen („Es regnet,“ „Peirce starb in Armut“), sondern Prädikate im Sinn der Prädikatenlogik (Näheres siehe dort), gegebenenfalls abgekürzt zu Prädikatbuchstaben (F, G, H,…). Ein Prädikat im Sinn der Prädikatenlogik ist eine Folge von Wörtern mit klar definierten Leerstellen, die zu einem Aussagesatz wird, wenn man in jede Leerstelle einen Eigennamen einsetzt. So ist zum Beispiel die Wortfolge „_ starb in Armut“ ein Prädikat, weil daraus der Aussagesatz „Peirce starb in Armut“ entsteht, wenn man den Eigennamen „Peirce“ in die Leerstelle einträgt. Ebenso ist die Wortfolge „_₁ ist reicher als _₂“ ein Prädikat, weil daraus die Aussage „Sokrates ist reicher als Platon“ entsteht, wenn man in die Leerstellen die Eigennamen „Sokrates“ bzw. „Platon“ einsetzt.

Notation der Betagraphen

Das grundlegende Sprachmittel ist die Identitätslinie („line of identity“), eine dick gezeichnete Linie beliebiger Form. Die Identitätslinie dockt an die Leerstelle eines Prädikats an, um zu zeigen, dass das Prädikat auf mindestens ein Individuum zutrifft. Um auszudrücken, dass das Prädikat „_ ist ein Mensch“ auf mindestens ein Individuum zutrifft – um also zu sagen, dass es (mindestens) einen Menschen gibt –, schreibt man demnach eine Identitätslinie in die Leerstelle des Prädikats „_ ist ein Mensch:“

Es gibt mindestens einen Menschen.
Prädikatenlogik: ∃xMensch(x)

Verbindet eine Identitätslinie zwei oder mehrere Leerstellen – egal ob unterschiedlicher Prädikate oder desselben Prädikats –, dann drückt sie aus, dass es mindestens ein Individuum gibt, das – in die jeweilige Leerstelle geschrieben – jedes dieser Prädikate zugleich wahr macht. Ein einfaches Beispiel ist nachfolgender Betagraph. In diesem Graphen drückt die Identitätslinie aus, dass es mindestens ein Objekt gibt, das sowohl das Prädikat „_ ist Amerikaner“ als auch das Prädikat „_ starb in Armut“ zugleich erfüllt – mit anderen Worten, dass es mindestens einen Amerikaner gibt, der in Armut starb.

Mindestens ein Amerikaner starb in Armut.
Prädikatenlogik: ∃x(Amerikaner(x)∧Starb-in-Armut(x))

Von diesem Betagraphen klar unterscheiden muss man den nachfolgenden, der nach den Regeln der Alphagraphen zusammengesetzt ist:

Es gibt mindestens einen Amerikaner. Mindestens ein Individuum starb in Armut.
Prädikatenlogik: ∃xAmerikaner(x) ∧ ∃yStarb-in-Armut(y)

In diesem Fall handelt es sich um zwei untereinander geschriebene einzelne Betagraphen. Der obere Teilgraph sagt aus, dass mindestens ein Individuum das Prädikat „_ ist Amerikaner“ erfüllt, d. h., dass es Amerikaner gibt. Der untere Teilgraph sagt analog aus, dass mindestens ein Individuum das Prädikat „_ starb in Armut“ erfüllt, d. h., dass mindestens ein Individuum in Armut starb. Zwei Betagraphen nebeneinander oder untereinander zu schreiben bedeutet nach den Regeln der Alphagraphen, die Wahrheit beider auszusagen. Der kombinierte Graph besagt demnach, dass es mindestens einen Amerikaner gibt und dass mindestens ein Individuum in Armut starb – er behauptet aber nicht, dass auf die Individuen, auf die das eine Prädikat zutrifft, auch das andere Prädikat zutrifft.

Durch geeignete Kombination der Identitätslinie mit den bekannten aussagenlogischen Mitteln der Alphagraphen lassen sich bereits fast alle prädikatenlogischen Aussagen formulieren.

Ein einfacher Fall ist das Verneinen einer Existenzaussage. Im folgenden Beispiel wird die Aussage des ersten Beispiels, d. h., die Aussage, dass es Menschen gibt, verneint, indem sie innerhalb eines Cuts geschrieben wird. Es wird also ausgesagt, dass es nicht der Fall ist, dass es Menschen gibt – in schönerem Deutsch: Dass es keine Menschen gibt.

Es gibt keine Menschen
Prädikatenlogik: ¬∃xMensch(x)

Von diesem Graphen unterscheidet sich der nachstehende, bei dem die Identitätslinie aus dem Cut herauszuragen scheint:

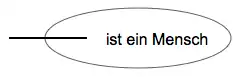
Es gibt mindestens ein Individuum, das kein Mensch ist.
Prädikatenlogik: ∃x¬Mensch(x)

Nach der Lesart der Betagraphen liegt hier die Verbindung zweier Graphen vor: Einer äußeren, leeren Identitätslinie, die schlicht besagt: „Etwas existiert;“ und einer Identitätslinie innerhalb des Cuts, der für sich aussagt: Es ist nicht der Fall, dass es mindestens ein Individuum gibt, das das Prädikat „_ ist ein Mensch“ erfüllt. Die Verbindung beider Linien in jenem Punkt, in dem sie den Cut schneiden, drückt die Identität der gegenständlichen Individuen aus: „Es gibt etwas, und dieses Etwas ist kein Mensch.“ So drückt obiger Betagraph nichts anderes aus als die Aussage, dass es Dinge gibt, die keine Menschen sind.

Ebenso gut lässt sich eine innerhalb eines Cuts liegende Identitätslinie mit einer äußeren Identitätslinie verbinden, die ihrerseits an ein Prädikat andockt. Der nachstehende Graph ist ein Beispiel für diese Konstellation. Für sich alleine genommen sagt der Cut aus: Es ist nicht der Fall, dass es ein Individuum gibt, das in Armut starb; und für sich alleine genommen sagt der äußere Ausdruck aus, dass es mindestens ein Individuum gibt, das Amerikaner ist. Da beider Ausdrücke Identitätslinien einander im Cut berühren, drückt der Gesamtausdruck die Identität beider Individuen aus, sagt also: Es gibt mindestens einen Amerikaner, der nicht in Armut starb.

Es gibt mindestens einen Amerikaner, der nicht in Armut starb
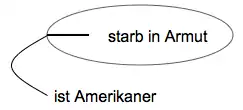
Prädikatenlogik: ∃x(Amerikaner(x)∧¬Starb-in-Armut(x))

Eine Allaussage vom Typ „Alle Schweine sind rosa“ würde durch einen Betagraphen des nachstehenden Typs dargestellt. Wörtlich handelt es sich hierbei um die Verneinung eines Satzes vom Typ des vorangehenden Beispiels, konkret um die Verneinung von „Es gibt mindestens ein Schwein, das nicht rosa ist.“ Zu verneinen, dass es nicht-rosa Schweine gebe, bedeutet nun aber auszusagen, dass alle Schweine tatsächlich rosa sind.

Alle Schweine sind rosa.
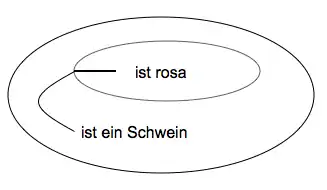
Prädikatenlogik: ∀x(Schwein(x)→Rosa(x)) bzw. wörtlich ¬∃x(Schwein(x)∧¬Rosa(x))

Ist eine Identitätslinie wie im folgenden Beispiel mit einem leeren Cut markiert, so drückt das die Nichtidentität der Individuen aus, die jene Leerstellen erfüllen, an denen die Identitätslinie andockt. In diesem Sinn sagt nebenstehendes Beispiel aus, dass es mindestens ein Schwein gibt und dass es mindestens ein rosa Individuum gibt, die aber beide nicht identisch sind.

Es gibt mindestens ein Schwein, und es gibt mindestens ein rosa Ding, die nicht identisch sind.
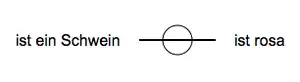
Prädikatenlogik: ∃x∃y(Schwein(x)∧Rosa(y)∧¬x=y)

Analog zum vorangehenden drückt der nachstehende Betagraph aus, dass es mindestens zwei Schweine gibt: „Es gibt ein Schwein, und es gibt (noch ein) Schwein, das mit ersterem nicht identisch ist.“

Es gibt mindestens zwei Schweine.
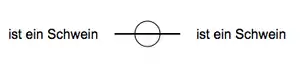
Prädikatenlogik: ∃x∃y(Schwein(x)∧Schwein(y)∧¬x=y)

Schlussregeln der Betagraphen

Beim System der Betagraphen werden keine genuin prädikatenlogischen Schlussregeln hinzugefügt, sondern es werden die bestehenden Regeln modifiziert. Im Einzelnen erhalten die bekannten Schlussregeln damit folgenden neuen Wortlaut:[14]

R1 – Löschregel („Rule of Erasure“): Jede Aussage, die auf geradzahliger Ebene liegt, und jeder Teil einer Identitätslinie, der auf geradzahliger Ebene auftritt, darf ersatzlos gestrichen werden.

Eine Anwendung der Löschregel (R1)

R2 – Einfügungsregel („Rule of Insertion“): Auf ungeradzahliger Ebene darf jede beliebige Aussage eingefügt werden und dürfen zwei oder mehrere unverbundene Enden von Identitätslinien beliebig miteinander verbunden werden.

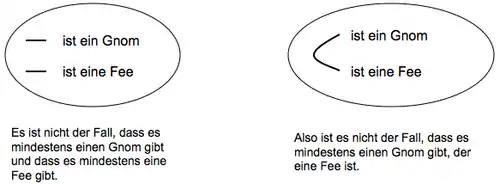Eine Anwendung der Einfügungsregel (R2)

R3 – Wiederholungsregel („Rule of Iteration“)

Jede Aussage, die Teil einer zusammengesetzten Aussage ist, darf auf derselben Ebene oder auf tieferer Ebene wiederholt werden, jedoch nicht innerhalb ihrer selbst. Für Identitätslinien sind folgende Iterationen zulässig:

An eine bestehende Identitätslinie darf jederzeit eine zusätzliche Identitätslinie mit losem Ende angefügt werden, d. h. eine Identitätslinie, die an keine Leerstelle eines Prädikats und an keine andere Identitätslinie andockt. Die so angefügte Identitätslinie darf jedoch keinen Cut berühren oder kreuzen.
Jede Identitätslinie mit losem Ende darf so verlängert werden, dass ihr neues Ende auf derselben oder auf tieferer Ebene zu liegen kommt.
Die Iteration einer Aussage und die Iteration einer Identitätslinie dürfen dergestalt miteinander kombiniert werden, dass das lose Ende der iterierten Identitätslinie mit der iterierten Aussage verbunden wird.

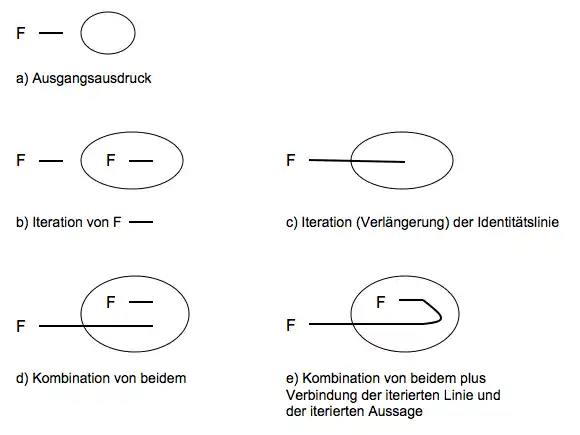Anwendungen der Wiederholungsregel (R3)

R4 – Aufhebung der Wiederholung („Rule of Deiteration“): Wenn eine Aussage X formal von einer Gestalt ist, dass sie aus einer Aussage Y durch Anwendung von R3, der Wiederholungsregel, entstanden sein könnte, dann darf mittels R4 von X auf Y geschlossen werden; es ist dazu nicht erforderlich, dass X tatsächlich durch eine Anwendung von R3 entstanden ist.

R5 – Regel des doppelten Cut („Rule of the Double Cut“): Doppelte Cuts dürfen nach Belieben eingefügt und gestrichen werden, sowohl um bestehende Aussagen herum als auch für sich alleine. Doppelte Cuts dürfen auch so eingefügt werden, dass sie Identitätslinien schneiden, es müssen dabei jedoch stets beide eingefügten Cuts alle geschnittenen Linien schneiden.

Weitere Beispiele

Beispiele

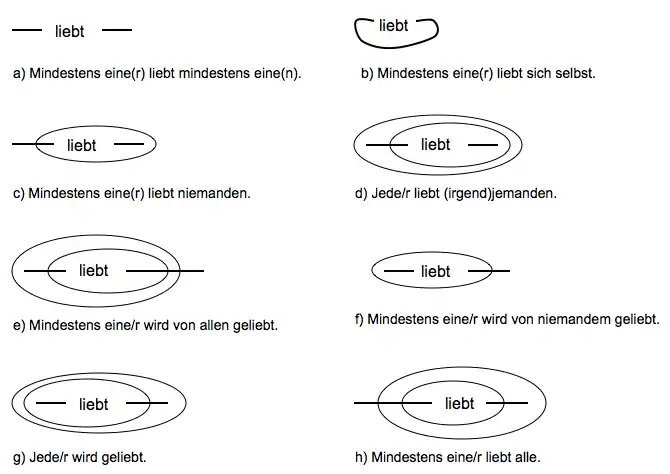
Quellen

„Development of first-order logic independently of Frege, anticipating prenex and Skolem normal forms“ (Hammer 1998, Seite 489)
„Peirce wants a sign which will not merely be conventionally understood […], but which will ″wear its meaning on its sleeve,″ so to speak“ (Zeman 1964, Seite 21, zitiert nach der Online-Ausgabe)
„[algebraic formulas] are not ‚iconic‘ – that is, they do not resemble the objects or relationships they represent. Peirce took this to be a defect.“ (Roberts 1973, Seite 17)
„[Peirce’s] graphical publications were few and not easy to understand, as he admitted himself.“ (Roberts 1973, Seite 12)
„[T]he syntax of Peirce’s graphs lacks, at least in general, the combinatorial elegance and simplicity of linear notations“ (Hammer 1998, Seite 502)
Roberts weist darauf hin, dass selbst das Standardwerk zur Geschichte der Logik, Kneale/Kneale: The Development of Logic. Clarendon Press. Oxford 1962, ISBN 0-19-824773-7, die logischen Diagramme Peirce’ nicht erwähnt.
„One questions the efficacy of Peirce’s diagrams […]. Their basic machinery is too complex […].“ (Quine: Review of Collected Papers of Charles Sanders Peirce, Volume 4: The Simplest Mathematics, Isis 22, Seite 552, zitiert nach Roberts 1973, Seite 13)
„Aside from their historic interest, Peirce’s graphical formalisms are of current interest. Sowa’s system of conceptual graphs […] is based on Peirce’s work. [Other work] also indicates increasing interest in the logic of graphical reasoning.“ (Hammer 1998, Seite 489)
siehe z. B. Sun-Joo Shin: „Reconstituting Beta Graphs into an Efficacious System“, Journal of Logic, Language and Information archive, Volume 8, Issue 3, Juli 1999, Seite 273–295
Die Beweise hierfür lieferte 1964 J. Jay Zeman in seiner Dissertation (siehe Literaturliste); für die Alphagraphen siehe auch die Arbeit von White, 1984
Genauer, aber nicht ganz so verständlich: damit, dass das „fundamental symbol“ (Grundzeichen) der Betagraphen eine „relation of existence“ (Existenzrelation) ausdrückt (zitiert nach Roberts, Seite 30)
Brief an William James, 18. Dezember 1897, zitiert nach Roberts, Seite 30
Die Darstellung der Schlussregeln und ihre Nummerierung folgt der Darstellung in Don D. Roberts Buch The Existential Graphs of Charles S. Peirce, Seite 40–45.
Die Darstellung folgt besonders eng Roberts, Seite 56–60

Literatur

Primärliteratur

Charles Hartshorne, Paul Weiss (Hrsg.): The Collected Papers of C. S. Peirce, Cambridge: Harvard 1931–35 (Nachdruck von Band 3 und Band 4: Harvard University Press 1987, ISBN 0-674-13801-5) – insbesondere Seiten 320–470 und 530–572 von Band IV. Online verfügbar sind:

Monographien

Don D. Roberts: The Existential Graphs of Charles S. Peirce, The Hague: Mouton 1973 (=Approaches to Semiotics 27) – das Standard-Einführungswerk zu den Existential Graphs, in englischer Sprache
Sun-Joo Shin: The Iconic Logic of Peirce’s Graphs, Cambridge, Massachusetts: MIT Press, Bradford 2002, ISBN 0-262-19470-8 – jüngste Monographie zum Thema
J. Jay Zeman: The Graphical Logic of C. S. Peirce, Chicago: 1964 (Dissertation), online verfügbar unter – bahnbrechende, stark formale Darstellung, in der unter anderem die Vollständigkeit und Korrektheit von Alpha- und Betagraphen gezeigt wird

Artikel

Eric M. Hammer: Semantics for Existential Graphs, Journal of Philosophical Logic, Volume 27, Issue 5 (Oktober 1998), Seite 489–503
Dennis Higgins, Bram Van Heuveln, Elizabeth Hatfield, Deborah Kilpatrick, Lut Wong: „A Java implementation for Peirce’s existential graphs,“ Journal of Computing Sciences in Colleges, Volume 16 Issue 3, März 2001, online kostenpflichtig unter – behandelt zwar eine Java-Implementierung, bietet aber einleitend eine kompakte Einführung in die Alphagraphen
Richard B. White: „Peirce’s Alpha Graphs: The Completeness of Propositional Logic and the Fast Simplification of Truth Functions,“ Transactions of the Charles S. Peirce Society, Volume 20, Number 4, 1984, Seite 351–361

Weblinks

Commons: Existential graphs – Sammlung von Bildern, Videos und Audiodateien

Eric Hammer: Peirce's Deductive Logic. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Mary Keeler: The Philosophical Context of Peirce's Existential Graphs
Existential Graphs MS 514 by Charles Sanders Peirce with commentary by John F. Sowa (englisch)
Peirce Edition Project (englisch)
Peirce-Beweisbauer – ein Java-Applet zum interaktiven Beweisen in Peirce’ System der Alphagraphen
Homepage von Dr. Frithjof Dau mit umfangreichem Material zum Thema Existential Graphs (unter anderem mit Scans der originalen Notizen von Peirce über die Existential Graphs MS 145)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] „Development of first-order logic independently of Frege, anticipating prenex and Skolem normal forms“ (Hammer 1998, Seite 489)

[2] „Peirce wants a sign which will not merely be conventionally understood […], but which will ″wear its meaning on its sleeve,″ so to speak“ (Zeman 1964, Seite 21, zitiert nach der Online-Ausgabe)

[3] „[algebraic formulas] are not ‚iconic‘ – that is, they do not resemble the objects or relationships they represent. Peirce took this to be a defect.“ (Roberts 1973, Seite 17)

[4] „[Peirce’s] graphical publications were few and not easy to understand, as he admitted himself.“ (Roberts 1973, Seite 12)

[5] „[T]he syntax of Peirce’s graphs lacks, at least in general, the combinatorial elegance and simplicity of linear notations“ (Hammer 1998, Seite 502)

[6] Roberts weist darauf hin, dass selbst das Standardwerk zur Geschichte der Logik, Kneale/Kneale: The Development of Logic. Clarendon Press. Oxford 1962, ISBN 0-19-824773-7, die logischen Diagramme Peirce’ nicht erwähnt.

[7] „One questions the efficacy of Peirce’s diagrams […]. Their basic machinery is too complex […].“ (Quine: Review of Collected Papers of Charles Sanders Peirce, Volume 4: The Simplest Mathematics, Isis 22, Seite 552, zitiert nach Roberts 1973, Seite 13)

[8] „Aside from their historic interest, Peirce’s graphical formalisms are of current interest. Sowa’s system of conceptual graphs […] is based on Peirce’s work. [Other work] also indicates increasing interest in the logic of graphical reasoning.“ (Hammer 1998, Seite 489)

[9] siehe z. B. Sun-Joo Shin: „Reconstituting Beta Graphs into an Efficacious System“, Journal of Logic, Language and Information archive, Volume 8, Issue 3, Juli 1999, Seite 273–295

[10] Die Beweise hierfür lieferte 1964 J. Jay Zeman in seiner Dissertation (siehe Literaturliste); für die Alphagraphen siehe auch die Arbeit von White, 1984

[11] Genauer, aber nicht ganz so verständlich: damit, dass das „fundamental symbol“ (Grundzeichen) der Betagraphen eine „relation of existence“ (Existenzrelation) ausdrückt (zitiert nach Roberts, Seite 30)

[12] Brief an William James, 18. Dezember 1897, zitiert nach Roberts, Seite 30

[13] Die Darstellung der Schlussregeln und ihre Nummerierung folgt der Darstellung in Don D. Roberts Buch The Existential Graphs of Charles S. Peirce, Seite 40–45.

[14] Die Darstellung folgt besonders eng Roberts, Seite 56–60