Engel-Kurve
Die Engel-Kurve bezeichnet in der Volkswirtschaftslehre und dort speziell in der Mikroökonomik eine mathematische Funktion, die – bezogen auf ein bestimmtes Gut – für jedes Einkommensniveau angibt, wie viele Einheiten ein Konsument optimalerweise von diesem Gut nachfragen sollte.[1]
Benannt ist die Engel-Kurve nach dem Statistiker Ernst Engel (1821–1896), der den Zusammenhang zwischen den Ausgaben, die ein Haushalt für Nahrungsmittel aufwendet, und dem Haushaltseinkommen untersuchte (der gefundene Zusammenhang firmiert in der Literatur als Engelsches Gesetz).[2]
Konstruktion
Der Engel-Kurve zugrunde liegt die so genannte Einkommens-Konsum-Kurve (auch: Einkommensexpansionspfad). Die Einkommens-Konsum-Kurve gibt – Zwei-Güter-Fall vorausgesetzt – in einem x1-x2-Diagramm alle Güterkombinationen an, die für ein bestimmtes Einkommensniveau optimal (d. h. nutzenmaximierend) sind. Die Einkommens-Konsum-Kurve ergibt sich entsprechend daraus, dass man bei gegebenen Güterpreisen und gegebenen Präferenzen das verfügbare Einkommen des Haushalts variiert, das resultierende Optimum jeweils einzeichnet und aus all den erhaltenen Optimalpunkten einen entsprechenden Kurvenzug konstruiert.
Die Engel-Kurve gibt demgegenüber keine Beziehung zwischen Gut 1 und Gut 2 an, sondern zwischen der Menge eines Gutes und dem verfügbaren Einkommen. Um sie zu erhalten, muss man lediglich die entsprechende Koordinate eines jeden Punktes der Einkommens-Konsum-Kurve mit dem Einkommensniveau zusammenbringen, aus dem er hervorgegangen ist. Die hieraus jeweils resultierenden Paare (y,x1) bzw. (y,x2) werden anschließend in einen eigenen Graphen übertragen; ihre Verbindung ergibt die Engel-Kurve.
Grundsätzlich wird das Einkommen auf der horizontalen Achse aufgetragen. Man dreht die Achsen aber regelmäßig aus Gründen der graphischen Konstruktion.[3]
Verlauf
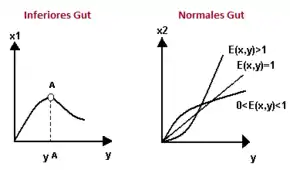
Am Verlauf der Engel-Kurve ist direkt ersichtlich, ob es sich bei einem Gut um ein normales Gut – d. h. ein Gut, dessen Nachfrage bei einer Einkommenserhöhung steigt – oder ein inferiores Gut – eines, dessen Nachfrage bei einer Einkommenserhöhung sinkt – handelt. In ersterem Fall ist die Engelkurve eine ansteigende Funktion, bei einem inferioren Gut fällt sie. Abb. 2 unterscheidet die folgenden Fälle:[4]
- Inferiores Gut: Die Engelkurve fällt im Einkommen (in der Graphik ist rechts von yA der inferiore Bereich); die Einkommenselastizität ist negativ.
- Normales Gut: Die Engelkurve steigt im Einkommen; die Einkommenselastizität ist positiv.
- Luxusgut: Die Engelkurve verläuft streng konvex (ein Anstieg des Einkommens um 1 % erhöht die Güternachfrage um mehr als 1 %); die Einkommenselastizität ist größer als 1.
- Homothetisches Gut: Die Engelkurve ist eine Ursprungsgerade, das heißt die Nachfrage ist proportional zum Einkommen (ein Anstieg des Einkommens um 1 % erhöht die Güternachfrage um genau 1 %); die Einkommenselastizität beträgt 1.
- Notwendiges Gut: Die Engelkurve verläuft streng konkav (ein Anstieg des Einkommens um 1 % erhöht die Güternachfrage um weniger als 1 %); die Einkommenselastizität liegt zwischen 0 und 1.
Siehe auch
Literatur
- Friedrich Breyer: Mikroökonomik. Eine Einführung. 5. Aufl. Springer, Heidelberg u. a. 2011, ISBN 978-3-642-22150-7.
- Arthur Lewbell: Engel curve. In: Steven N. Durlauf und Lawrence E. Blume (Hrsg.): The New Palgrave Dictionary of Economics. 2. Auflage. Palgrave Macmillan 2008, doi:10.1057/9780230226203.0476 (Online-Ausgabe).
- Hal Varian: Intermediate Microeconomics. A Modern Approach. 8. Aufl. W. W. Norton, New York und London 2010, ISBN 978-0-393-93424-3.
Einzelnachweise
- Vgl. Breyer 2011, S. 143 f.; Varian 2010, S. 97.
- Vgl. Lewbell 2008.
- Dazu illustrativ Breyer 2011, S. 144 (Abb. 4.11).
- Vgl. Varian 2010, S. 97 f., 101; Breyer 2011, S. 143 f.