Distanzvektoralgorithmus
Beim Distanzvektoralgorithmus (auch bekannt als Distanzvektor-Routing oder Distance Vector Routing) handelt es sich um ein dynamisches Routing-Protokoll, das nach dem Prinzip „Teile deinen Nachbarn mit, wie du die Welt siehst“ funktioniert und intern auf dem Bellman-Ford-Algorithmus basiert. Er wird von Routern in paketvermittelten Netzwerken eingesetzt und ist in IP-Netzen z. B. als RIP und IGRP implementiert. Distanzvektorprotokolle sind selbstorganisierend, vergleichsweise einfach zu implementieren und funktionieren nahezu ohne jede Wartung. Eine andere Art von Routing-Protokollen sind Link-State-Protokolle.
Prinzip
Das prinzipielle Vorgehen eines Distanzvektorprotokolls:
- Erzeuge eine Kostenmatrix, welche Router über welche Nachbarn und zu welchen Kosten erreichbar sind und anfangs nur die (bekannten) Kosten zu direkten Nachbarn enthält.
- Erzeuge eine Aufstellung mit Informationen, welche Router wir zu welchen Kosten am besten erreichen können und schicke sie an alle Nachbarn.
- Warte auf Aufstellungen dieser Art von anderen Routern, rechne diese dann in die eigene Kostenmatrix ein.
- Ändern sich dadurch die minimalen Kosten, zu denen wir einen Router erreichen können: fahre mit Schritt 2 fort, sonst mit Schritt 3.
Kosten sind gleichzusetzen mit Metrik. Jedes Routing-Protokoll nutzt eine andere Betrachtung für die Kosten einer Route. Bei RIP wird beispielsweise die Anzahl der Router zum Ziel ("Hop-Count") als einziger Kostenwert genutzt, d. h. die Bandbreite bleibt hier bei der Betrachtung unberücksichtigt.
Beispiel
Es existieren vier Router A–D und zwischen ihnen folgende Punkt-zu-Punkt-Verbindungen (Links):
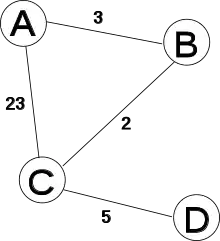
Im Folgenden sind die Kostenmatrizen der Router zu Beginn und nach jedem vollständigen Austausch von Datenpaketen dargestellt. Dabei ist der beste Pfad zu einem anderen Router jeweils grün, ein neuer bester Pfad – der im nächsten Schritt an die Nachbarn gesendet wird – gelb hinterlegt. Graue Felder markieren Werte die nicht betrachtet und daher nicht gepflegt werden. Diese Werte stünden entweder für die Distanz eines Routers zu sich selbst (betrifft Zeilen und Spalten) oder aber der betrachtete Router x ist kein direkter Nachbar zu einem anderen gelisteten Router z. Es wird nicht betrachtet wie hoch die Distanz von Router x zum Router y über ("via") den Router z ist (betrifft Spalten).
| T=0 |
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T=1 |
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T=2 |
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T=3 |
|
|
|
|
Erläuterung der Vorgänge im Router A:
- T=0: Wir erzeugen die initiale Kostenmatrix. Sie enthält nur unsere direkten Nachbarn B und C mit den uns bekannten Kosten. Wir schicken daraufhin unsere neuen besten Pfade (B mit Kosten 3, C mit Kosten 23) an unsere direkten Nachbarn
- T=1: Wir haben von den Routern B und C Datenpakete erhalten und wissen jetzt, zu welchen Kosten wir D und wie wir C und B jeweils auch erreichen können. Im Fall der Zielrouter C und D ist das sogar ein neuer bester Pfad, den wir im nächsten Schritt an unsere Nachbarn übertragen werden
- T=2: Wir haben von Router B ein Datenpaket erhalten und wissen jetzt, dass B den Router D günstiger erreichen kann. Wir tragen die Kosten in unsere Matrix ein und werden diesen neuen besten Pfad wieder an unsere Nachbarn verbreiten.
- T=3: Wir haben keine neuen Informationen mehr empfangen; unsere besten Pfade haben sich nicht geändert und wir senden keine neuen Informationen an unsere Nachbarn. Denen geht es genauso, der Algorithmus terminiert.
Probleme

Ein Problem des Distanzvektoralgorithmus ist das Zählen bis Unendlich, der sogenannte Count-To-Infinity-Effekt.[1] Dieser lässt sich an folgendem Beispiel zeigen.
Gehen wir davon aus, dass sich der Link von C nach D drastisch verschlechtert und betrachten die Situation aus der Sicht von Router A:
- Wir empfangen von C die Meldung, dass D über ihn nur noch sehr schlecht zu erreichen ist. Das ändert jedoch nichts an unserem besten Pfad, der ja über B führt.
- Bald bekommen wir aber auch von B die Meldung, dass D über ihn nur noch sehr schlecht zu erreichen sei – die Pfadkosten seien auf 13 = 3 + 10 = 3 + 3 + 2 + 5 angestiegen. Dass die Kosten nicht deutlich höher angesetzt wurden liegt daran, dass B ja noch eine indirekte Route kannte, die zu D führt: die Route B–A–B–C–D. Und A gab ja nach bestem Wissen an, er könne D zu den Kosten 10 erreichen.
- Nun haben sich aber unsere Pfadkosten zu D geändert. Weil B den Router D nur noch zu Kosten von 13 erreichen kann, können auch wir D nur noch zu Kosten von 16 erreichen.
- Dadurch ändert sich aber wieder unser bester Pfad, was wir gleich wieder B mitteilen – die Pfadkosten werden langsam hochgezählt statt sprunghaft zu steigen.
Das Zählen bis Unendlich lässt sich bei direkten Schleifen zwischen zwei Routern relativ leicht vermeiden. Eine Pfadinformation darf nicht über dasselbe Interface veröffentlicht werden, worüber sie empfangen wurde. Dieses Verfahren nennt man Split-Horizon.
Im Fall von längeren Schleifen ist eine Lösung des Problems nicht mehr trivial. In Distanzvektorprotokollen gilt allgemein, dass sich Nachrichten über die Erhöhung der Kosten nur langsam verbreiten. Um auch diesem Problem Herr zu werden, werden das Poisoned-Reverse-Verfahren und so genannte Triggered Updates verwendet: Findet ein Router heraus, dass ein Nachbar nur noch schwer oder gar nicht mehr erreichbar ist, veröffentlicht er diese Tatsache sofort aktiv im Netz.
In einer Abwandlung des Distanzvektoralgorithmus, dem sogenannten Distance-Path-Algorithmus den z. B. BGP implementiert, ließe sich das Problem von Schleifen leichter lösen. Dieser Algorithmus speichert neben dem nächsten Hop auch noch den gesamten restlichen Pfad zum Zielrouter. So lassen sich neben dem Kriterium „günstigste Route“ auch leicht andere Kriterien, z. B. firmenpolitische Maßgaben, umsetzen.
RIP-Versionen
Für IPv4 liegen zwei Versionen von RIP vor: RIPv1 und RIPv2. In RIPv1 sind keine Subnetzmasken implementiert.
Für IPv6 wurde RIP angepasst und unter der Bezeichnung RIPng veröffentlicht.
Siehe auch
Ein anderes Routing-Verfahren ist das Link-State- und das Pfad-Vektor-Routing.
Literatur
- James F. Kurose, Keith W. Ross: Computernetzwerke: Der Top-Down-Ansatz, Pearson Studium, 4. aktualisierte Auflage (1. September 2008), ISBN 978-3827373304, S. 425.
Einzelnachweise
- Andrew S. Tanenbaum: Computernetzwerke, Pearson Studium, 4. überarbeitete Auflage (15. Juli 2003), ISBN 978-3827370464, S. 397.