Diffusor (Akustik)
Unter einem Diffusor versteht man in der Akustik ein Bauelement, das einfallende Schallwellen zerstreuen und die unerwünschte Wirkung des ansonsten gleichförmig reflektierten Schalls vermindern soll. Durch Diffusoren werden die Schallwellen sowohl quantitativ, als auch qualitativ im Raum gleichmäßiger verteilt. Wenn die auf diese Weise mehrfach reflektierten Wellen später auf das Ohr treffen, kommen die einzelnen Frequenzen ungeordnet aus unterschiedlichen Richtungen, was die Lokalisation der ursprünglichen Schallquelle erschwert. Dadurch ändert sich der Raumeindruck.
Anwendungsgebiete


Haupteinsatzbereiche von Diffusoren ist die Verbesserung der Raumakustik in Auditorien, Konzerthallen sowie in Regie- und Aufnahmeräumen in Tonstudios. Auch in technischen Messräumen zur Beurteilung der Qualität von Lautsprechern sowie zur bewerteten Lärmmessung an industriellen Geräten sind sie zu finden. In jüngster Zeit finden sich Diffusoren auch vermehrt in HIFI-Hörräumen privater Anwender.[1]
Durch die Lenkung und frequenzabhängige Streuung der Schallwellen können in diesen Räumen unterschiedliche Bereiche geschaffen werden, in denen der durch eine Klangquelle emittierte Schall quantitativ zu einem gewünschten Anteil aufrechterhalten wird, ohne dass es zur Bildung von Raummoden kommt. Zudem wird die Wirkung der Reflexion an Wänden teilweise aufgehoben, wodurch die Raumgröße und dessen Beschaffenheit nicht mehr so aufdringlich ist, bzw. scheinbar verschwindet und sich die Hörsamkeit verbessert. Besonders Sprache und andere höherfrequente Klanganteile können so besser wahrgenommen werden.[2] In kleinen Räumen, in denen es bei gleicher Laufzeit und Schallabschwächung zu mehr Reflexionen kommt, sind Diffusoren besonders wirksam.[3]
In Tonstudios macht man sich dies zunutze, um die subjektive Größe eines Raumes, wie sie in den Tonsignalen des Stereosystems abgebildet ist, unbeeinflusst durch die tatsächliche Größe des Studios abzuhören. Typischerweise befinden sich Diffusoren im nicht bedämpften Bereich des Abhörraums (siehe Live End Dead End). Diffusoren stehen damit im Gegensatz zu den in Studios ebenfalls angewendeten Absorbern, welche den Schall dämpfen sollen.
In großen Konzerthallen und Opernhäusern wird Diffusion auch dadurch bewerkstelligt, dass entsprechende Bauelemente ungleichförmig angeordnet und geeignet in das Gesamtraumkonzept integriert werden. Dies betrifft neben der treppenförmigen Anordnung von Bestuhlung und Tribünen auch die Gestaltung von Schallreflektoren über den Musikern im Orchesterbereich. Moderne Theater und Konzerthallen werden dazu mithilfe aufwändiger Schallanalysen unter Nutzung von Simulationssoftware geplant.[4]
Funktion


Die wesentliche Arbeitsweise von Diffusoren besteht darin, Teile der Schallwelle, die an unterschiedlichen Stellen eintreffen, in unterschiedliche Richtungen zu lenken, statt sie einfach gemäß dem gespiegelten Einfallswinkel zurückzuwerfen, wie es an einer glatten Wand der Fall gewesen wäre. Dies wird sowohl durch Verdrehen von Teilen der Verkleidung, als auch durch Erhöhungen und Vertiefungen im Material erreicht. Durch die entstehenden Unebenheiten werden, abhängig von der Wellenlänge 2 unterschiedliche Effekte genutzt:
Für Schallanteile, deren Wellenlänge deutlich geringer ist, als die Größe des verdrehten Teilelementes, erfolgt eine direkte Reflexion des Wellenpakets anhand des Reflexionsgesetzes. Die Ablenkung erfolgt dabei gemäß der Ausrichtung der Teilfläche. Die Schallwelle wird gewissermaßen zerstückelt.

Durch die Überlagerung der Reflexionen aufgrund unterschiedlichen Vertiefungen kommt es wiederum zu Interferenzeffekten: Dabei überlagern sich Wellen unterschiedlicher Frequenzen und es kommt in Abhängigkeit ihrer Wellenlänge und dem durch die Vertiefung vorgegebenen Phasenversatz zu teilweisen Auslöschungen und Verstärkungen. Betrachtet man die Maxima und Druckgradienten der neu entstehenden Welle, werden diese in unterschiedliche Richtungen gelenkt. Dies gilt vor allem für die direkt aus der 90°-Grad-Richtung einfallenden Welle, die ansonsten direkt zurückgeworfen würde.
Diffusion eignet sich damit in erster Linie für mittlere und hohe Frequenzen, weil für Bässe unakzeptable Bautiefen erforderlich wären.
Bauformen
1D-Diffusoren
Eindimensionale Diffusoren sind entlang einer Achse gleichförmig aufgebaut und arbeiten mit beiden Funktionsprinzipien. In der Regel sind sie entgegen der Hörachse ausgerichtet, d. h. die Vertiefungen verlaufen in der Draufsicht vertikal. Damit erfolgt eine starke Verteilung der Frequenzen auf der horizontalen Stereobasis.

Einige Bauformen machen sich überwiegend die Interferenz zunutze. Sie sind auf eine bestimmte Frequenz hin optimiert, indem die relativen Tiefen auf eine bestimmte Wellenperiode angepasst werden. Für diese Frequenz ist der Diffusor dann besonders stark wirksam, was allerdings dazu führt, dass in der Nähe des Diffusors einzelne Frequenzen stark betont wahrgenommen werden können.
Es existiert eine Reihe von Möglichkeiten, zu Zahlenkombinationen zu gelangen, die zu einem mehr oder weniger statistischen Streuverhalten führen.
Quadratic Residue Diffusers (QRD)
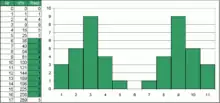
Eine sehr bekannte Bauform ist die nach Manfred Schroeder benannte Form des „Schroederdiffusors“. Er ist rechteckig gebaut und besteht aus einzelnen, durch Zwischenwände abgetrennte Kammern unterschiedlicher Tiefe, die auf eine bestimmte Wellenlänge angepasst sind.[5] Das Konzept basiert auf der Theorie, dass die Wellen dann am besten gestreut werden, wenn für die Tiefe der Kammern eine wiederkehrende Struktur auf der Basis einer Zahlenfolge verwendet wird, die Bruchteilen der Wellenlänge entsprechen. Dabei wird die Nummer der Vertiefung aufsteigend quadriert und der mathematische Rest, das sogenannte "Residuum" gebildet, der bei der Division durch eine Primzahl entsteht. Der Verlauf der Tiefen entspricht damit der einer Parabel mit jeweils um volle Perioden versetzten Ästen. Daher heißen Diffusoren dieses Typs auch QRD (quadratic residue diffusor).
QR-Diffusoren sind naturgemäß symmetrisch um einen dedizierten Punkt herum. Damit kann mit nur einem einzigen Bauelement in der Mitte eines Raumes ein symmetrisches Stereobild aufrechterhalten werden.
Der Aufbau kann auch invertiert erfolgen, d. h. indem Tiefen und Höhen vertauscht werden, weil auch dann die Wellenperioden entsprechend agieren.
Manchmal findet man QRD, bei denen die Zwischenstege weggelassen wurden. Damit wird die Wirkung stark abgeschwächt, weil die verzögert rückgeworfenen Wellenpakte nicht mehr so konzentriert sind. Andererseits kann dies bei geringen Distanzen zum Diffusor vorteilhaft sein, weil weniger deutliche Resonanzen entstehen, die in der Nähe stören könnten.
Cubic Residue Diffusers (CRD)
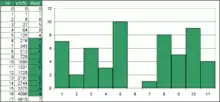
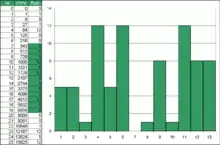
Eine ähnliche Methode besteht in der Anwendung der Kubikfunktion auf die Nummer des Elements, statt des üblichen Quadrats. Diese kubische Vorschrift erzeugt ein stärker gestreutes Abstrahlverhalten. CRD-Diffusoren sind für kleine Räume besser geeignet.[6]
Dabei entstehen jedoch innerhalb des Bauelements keine periodische Spiegelsymmetrie mehr, da die Kubikfunktion aus mathematischer Sicht eine ungerade Funktion ist. Da Räume in aller Regel ein symmetrisches Stereobild benötigen,[7] muss somit ein weiterer, spiegelsymmetrisch aufgebauter Diffusor verwendet werden.
Dieses Abstrahlverhalten ist aber bisher nicht hinreichend untersucht und die Bauform praktisch kaum verbreitet.
Maximum Length Sequence (MLS)

Ebenfalls sehr bekannt sind Geometrien nach der Methode der Maximum Length Sequence. Sie gehören ebenfalls zu den Schroeder-Diffusoren[8] und nutzen nur einen einzigen Wert für die Vertiefungen, welche aber unterschiedliche Breiten haben, die der Maximalfolge von Nullen und Einsen entspricht, die sich aus der Polynomdivision ergibt. Die Breite ist dabei kleiner oder gleich der halben Wellenlänge der Frequenz, auf die hin optimiert wird. Die Wirksamkeit ist gegenüber der bei QRDs jedoch eingeschränkt. Eine Wandstruktur aus MLS wirkt schmalbandiger.[9]
Primary Root Diffusoren (PRD)
Eine weitere Bauform sind sogenannte Primary Root Diffusoren, die auf Sequenzen einfacher Wurzeln basieren. Das Verhalten ist ähnlich dem der QRD.[10] Der Hauptunterschied besteht darin, dass der QRD Schallwellen behandelt, die nur von einer geometrischen Ebene kommen, während der PRD auch Schallwellen behandelt, die in zwei Ebenen eingehen, also von einer beliebigen Stelle im Raum kommen.[11]
Alternating Binary Frequency-Diffusoren (ABF)
Diese sind ähnlich den QRD-Diffusoren und stellen eine Kombination aus mehreren überlagerten Binärsequenzen dar.[12]
Mikroperforierte Diffusoren (MPD)
MPDs bestehen aus einzelnen, streifenförmig angeordneten Resonatoren, welche auf unterschiedlichen Resonanzfrequenzen schwingen. Infolge der daraus resultierenden unterschiedlichen Wandimpedanzen werden einfallende Wellen diffus reflektiert. Die Resonanzfrequenzen resultieren aus pseudostochastischen Zahlenfolgen.[13]
2D-Diffusoren

Sollen Schallwellen frequenzabhängig in alle Raumrichtungen gestreut werden, empfiehlt sich eine 2-dimensionale Anordnung, bei der quasi zwei 1D-Diffusoren orthogonal überlagert werden.[14] Dadurch werden die ankommenden Wellen noch ungeordneter gestreut, was sich besonders in kleinen Studios und Regieräumen als vorteilhaft erweisen kann. Im Gegensatz zu anderen Diffusoren streuen zweidimensionale Diffusoren den Schall in einem halbkugelförmigen Muster. Dies geschieht durch ein Gitter, dessen Hohlräume Vertiefungen unterschiedlicher Ausprägung aufweisen, entsprechend der Matrixaddition von zwei quadratischen Sequenzen, die denen eines regulären Diffusors entsprechen. Diese Diffusoren erlauben eine gute Steuerung der Diffusionsrichtung. Auch hier gibt es eine Reihe von diversen Konzepten mit unterschiedlichen Bauformen und Designmethoden. Aufgrund der Bauform, die an Wolkenkratzern erinnert, werden diese oft als Skyline-Diffusoren bezeichnet.[15] Der erste omnidirektionale 2D-Diffusor wurde 1990 von RPG patentiert. Im Jahre 1995 folgte der Skyline-Diffusor.[16]
Aus praktischen Gründen werden bei der 2-dimensionalen Version die Zwischenstege oft weggelassen, wodurch sich ein anderes Abstrahlverhalten ergibt, das nicht mehr mit den Schroederdiffusoren übereinstimmt.
QRD- / CRD-Diffusoren

Eine einfache Möglichkeit, symmetrische und periodische Anordnungen zu generieren, ist auch hier die QRD-Methode. Diese beruht auf der Modulo-Funktion, allerdings spielen hier beide Koordinaten eine Rolle und fließen in unterschiedlicher Weise in die Berechnung ein.[17] Je nach Berechnung und Versatz der Koordinaten ergeben sich abweichende Strukturen.
Statistische Diffusoren
Heute werden vermehrt empirisch gewonnene sowie statistisch verteilte Zahlen angenommen, um zu einer möglichst gleichförmigen Streuung zu gelangen. Eine Möglichkeit besteht darin, rückgekoppelte Gleichungen zu nutzen, wie sie bei der Erzeugung von CRC-Codes verwendet werden.[18]
Verwendung

Die durch die Berechnungsvorschriften entstehenden Zahlen sind entlang der Achsen meistens periodisch, d. h. die Struktur wiederholt sich. Mehrere der so entstehenden Elemente können aneinandergereiht werden. Hiermit wird der Effekt der sich überlagernden Wellenpakete zu einer neuen abgelenkten Welle verstärkt. Es empfiehlt sich, die Diffusion über eine gesamte Wand zu erstrecken und die Wände als Spiegel zu nutzen. Da Diffusoren eine definierte Abstrahlrichtung haben, können sie auch alternierend angebracht werden.[19]
Die neu erzeugte Schallwelle bildet sich aber erst in einer gewissen Distanz vom Diffusor vollständig aus, die umso größer ist, je tiefer die Designfrequenz des Diffusors liegt und je breiter der Diffusor ist. Daher ist bei der Platzierung des Diffusors auf ausreichenden Abstand zur Position des Hörenden zu achten. Es sollten etwa 20 % einer Fläche bedeckt sein, um eine signifikante Wirkung zu erlangen.[3]
Im HIFI-Bereich hat sich die Anbringung von Diffusoren im Bereich des Zwischenraumes hinter den Lautsprechern etabliert,[20] jedoch ist die Wirkung umstritten.[21] Eine Nutzung direkt hinter den Lautsprechern führt oftmals zu keiner großen Wirkung, weil Lautsprecher im relevanten Frequenzbereich vorwiegend nach vorn abstrahlen und somit auf dahinter stehende Diffusoren hauptsächlich der schon mehrfach reflektierte und daher bereits im Pegel abgeschwächte und zeitverzögerte Schallwellen treffen.[22]
Materialien
Diffusoren werden aus unterschiedlichen Materialien gefertigt. Es existieren Leichtbauversionen aus aufgeschäumtem Styropor, sowie Verbundsysteme aus Holz und sogar Metall. Hauptwerkstoff ist Holz, weil es keine ausgeprägte Neigung zum Eigenschwingen hat, eine hohe Eigendämpfung besitzt, gut zu verarbeiten- und dennoch schallhart genug ist. Eine genügend stark reflektierende Wirkung – insbesondere bei geringeren Frequenzen – ist die Voraussetzung für das Funktionieren der Diffusion und nur durch sehr schallhartes Material zu erreichen. Daher werden Diffusoren aus weichen Materialien wie EPS / XPS teilweise mit Epoxidharz gehärtet, um ihre Wirkung zu verbessern. Eintreffender Schall, der nicht reflektiert wird, wird entweder durch solche weichen Elemente absorbiert oder geht unbeeinflusst hindurch, siehe Transmission. Er trägt dann nicht zur Diffusion bei.
Räumliches Streuverhalten
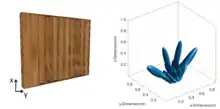
Einfache Berechnung und Betrachtung
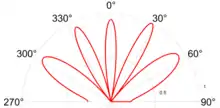
Die hinreichend bekannten und von Schroeder für akustische Diffusoren publizierten, analytischen Berechnungsverfahren zeigen den Zusammenhang zwischen der Oberflächenstruktur und der räumlichen Verteilung des Schalls: Die Abstrahlcharakteristik einer Oberfläche im akustischen Fernfeld kann z. B. durch Fouriertransformation der Oberflächenstruktur berechnet werden.[25]
Das Rechenergebnis lässt sich dann als Richtdiagramm darstellen. Es veranschaulicht das frequenzabhängige, räumliche Abstrahlverhalten der Oberfläche in einer Ebene.
Dabei ist zu beachten, dass dies für einen idealen perfekt strahlenden Diffusor gilt. In der Praxis ergeben sich durch Beugung und endliche Größe der Oberflächen davon abweichende Effekte.
Dreidimensionale Berechnung und Betrachtung
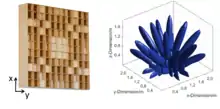
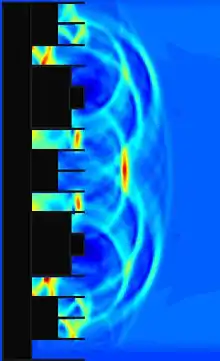
Die vollständige Berechnung des akustischen Verhaltens eines Diffusors ist, basierend auf der Superposition akustischer Monopole, nach dem huygensschen Prinzip möglich. Dadurch kann die dreidimensionale Schalldruckverteilung bei unterschiedlichen Frequenzen in allen Raumrichtungen berechnet und visualisiert werden.
Im Vergleich zu der eindimensionalen Bauweise wird die räumlich erweiterte Streuwirkung zweidimensionaler Diffusoren deutlich. Es ist zu erkennen, dass durch einen zweidimensionalen QRD eine dreidimensional ausgeglichene Schallstreuung erreicht werden kann.
Weitere Anwendungen
Microdiffusor
Die Methode der Diffusion von Schallwellen mittels Schröder-Diffusoren wird auch auf mikroskopisch feinstrukturierten Oberflächen angewendet, um spezielle Hochfrequenzbauelemente zu erzeugen.[28]
Weblinks
- Walker, Eng (BBC): Design und Anwendung akustischer Diffusion
- Dr. Jörg Hunecke: Funktionsprinzip Diffusoren
- Bill "Collo" Collison: Freie Konstruktionssoftware QRDude
- Arqen Sonic: Freie Blaupausen für Diffusoren
- Alexander Ulz: Akustische Diffusoren
- Jürgen Schuhmacher: Unterschiedliche Diffusorkonzepte
- David Browne: Nutzen von akustischer Diffusion
- Fischer / Stens: akustische Maßnahmen im Selbstbau
- Torben Bostelmann: Akustik Diffusor – Wirkung & Funktion
- HX AUDIO LAB: Diffusorberechnung und Erklärungen
- Heimkinopraxis: Funktionsweise, Berechnung und Selbstbau
- Dr. Benedikt Kohout über Akustik, Studiomagazin
- DEGA: Wellen und Felder in der Akustik
- Universität Aachen: Virtuelle Akustik – Simulation von Diffusion und Absorption
Literatur
- Handbuch der Elektroakustik; Günther Boye, Urbi F. Herrmann; Hüthig Buch Verlag Heidelberg; ISBN 3-7785-1575-6.
- EMPA/HSR-Tagung 2001; "Holz in der Raumakustik"; Autor: Kurt Eggenschwiler
- Acoustic Absorbers and Diffusers: Theory, Design and Application, Dr Trevor Cox, Dr Peter D'Antonio CRC Press, 2004, ISBN 0-415-29649-8.
Referenzen
- Farshid Shahlawandian: Der LowBeats HiFi Hörraum: hier hört man alles. Low Beats, November 2017, abgerufen am 9. Juli 2020.
- Klaus Burosch: Der Hörraum bei mittleren und hohen Frequenzen. Burosch, abgerufen am 14. Juli 2020.
- Jeff Hedback: Diffusion ein Wunderbares Hilfsmittel. GIK, 1. Juni 2009, abgerufen am 14. Juli 2020.
- Alfred Schmitz, Anselm Goertz: Planung von Räumen. (PDF) DEGA Akademie Raumakustik und Beschallung, 2012, abgerufen im Jahr 2020.
- BauNetz: Schroeder-Diffusoren (Prinzip) | Akustik | Schallreflexion | Baunetz_Wissen. Abgerufen am 9. Juli 2020.
- Juergen Schuhmacher: Cubic Residue Diffusers. 96khz, 20. April 2015, abgerufen am 20. April 2015 (englisch).
- Jörg Bohne: Regeln und Tipps. In: bohne-audio.com. 12. Oktober 2017, abgerufen am 12. Oktober 2017.
- Dr. Jörg Huneke: Diffusoren. Abgerufen am 9. Juli 2020.
- Andreas Melcher: Schallstreuung mit Phasengittern. AM Acoustic, 2020, abgerufen am 14. Juli 2020.
- Alexander Ulz: Akustische Diffusoren. (PDF) TU Graz, abgerufen im Jahr 2020.
- Desiderata: The PRD panel. In: http://desiderata.xyz/. 13. Juni 2016, abgerufen am 10. Juli 2020 (amerikanisches Englisch).
- 96kHz: Alternating Binary Frequency Diffusers. In: www.96khz.org. 2007, abgerufen am 14. Juli 2020 (englisch).
- Jörg Hunecke: Mikroperforierte Diffusoren (MPD). In: hunecke.de. Abgerufen am 14. Juli 2020.
- Hans Werner Strube: More on the diffraction theory of Schroeder diffusors, J. Acoust. Soc. Am. 70, 633 (1981), doi:10.1121/1.386757
- Nils Hitschke: Diffusoren: Funktionsweise, Berechnung und Selbstbau. In: Heimkino Praxis. 11. Februar 2018, abgerufen am 9. Juli 2020.
- Omnifusor. (PDF) In: http://www.rpgacoustic.com/. RPG, 1990, abgerufen im Jahr 2020 (englisch).
- Felix Baarß: FAQ Akustikelemente: Diffusor, Absorber, Bassfalle - delamar. In: www.delamar.de. 13. Juli 2015, abgerufen am 13. Juli 2015.
- P. Schulthess, M. Wende: Rechnernetze - CRC - Statistik. In: informatik.uni-ulm.de. 2002, abgerufen im Oktober 2020.
- Schuhmacher Jürgen: Quadratic residue diffusers. 96khz, 7. Mai 2003, abgerufen im Jahr 2020 (englisch).
- Stefan Gawlick: TechTalk - Diffusor + Resonator. FIDELITY online, 14. September 2014, abgerufen am 14. Juli 2020.
- Diffusor für wandnahen Lautsprecher, Akustik - HIFI-FORUM. Abgerufen am 23. Juli 2020.
- Floyd E. Toole: Sound Reproduction: The Acoustics and Psychoacoustics of Loudspeakers and Rooms. Hrsg.: Focal Press. Verlag Taylor & Francis Ltd., 2008, ISBN 0-240-52009-2, S. 570.
- Schroeder, Manfred R. "Binaural dissimilarity and optimum ceilings for concert halls: More lateral sound diffusion." The Journal of the Acoustical Society of America 65.4 (1979): 958-963.
- M. Schroeder: Binaural dissimilarity and optimum ceilings for concert halls: More lateral sound diffusion. 1979, doi:10.1121/1.382601 (semanticscholar.org [abgerufen am 5. Oktober 2020]).
- Schroeder, Manfred R. "Diffuse sound reflection by maximum− length sequences." The Journal of the Acoustical Society of America 57.1 (1975): 149-150.
- O. T. H. Amberg-Weiden: EASE - Samurai. Ostbayerische Technische Hochschule Amberg-Weiden, 2018, abgerufen am 31. Juli 2020.
- Jörn Hübelt: Messung und Simulation von Schallfeldern. In: hs-mittweida.de. 2020, abgerufen am 31. Juli 2020.
- Yifan Zhu, Xudong Fan, Bin Liang, Jianchun Cheng, Yun Jing: Ultrathin Acoustic Metasurface-Based Schroeder Diffuser. In: Physical Review X. Band 7, Nr. 2, 5. Juni 2017, S. 021034, doi:10.1103/PhysRevX.7.021034 (aps.org [abgerufen am 31. Juli 2020]).