D*-Algorithmus
Der D*-Algorithmus ist ein Suchalgorithmus. Es handelt sich um eine Erweiterung des A*-Algorithmus und somit einen direkten „Nachfahren“ des Dijkstra-Algorithmus. Sowohl A* als auch der Dijkstra-Algorithmus sind in ihrer Grundform unflexibel und können auf Veränderungen im Graphen während oder nach der Expansion nicht reagieren. In beiden Fällen kann der Anwender alle Ergebnisse verwerfen und nochmal von vorne beginnen. Gerade bei Arbeiten mit Robotern oder Agenten unter realen Bedingungen (begrenzte Sensorreichweite, unbekannte Umgebung) kommt es vor, dass große Karten ständig aktualisiert werden.
Anthony Stentz entwickelte an der Carnegie Mellon University eine Möglichkeit, A* so zu modifizieren, dass er mit den neuen Anforderungen funktioniert.
Verfahrensweise
Erst-Expansion
Wie bei A* wird auch bei D* zunächst der Weg vom Start zum Ziel gewählt. Anders als bei A* wird jedoch die Reihenfolge umgekehrt: vom Ziel zum Start. Das hat den Vorteil, dass jeder expandierte Knoten auf den nächsten zum Ziel führenden Knoten verweist und die exakten Kosten zum Ziel (nach der Expansion) kennt.
Je nachdem, ob eine fokussierende Metrik zur Unterstützung eingesetzt wird und ob nach dem Auffinden des Startpunktes abgebrochen wird, werden mehr oder weniger Punkte expandiert und stehen somit später als Unterstützung bereit. Das Expandieren läuft analog zu A*. Wird der Startknoten expandiert, kann der Algorithmus abgebrochen werden. Die OpenList darf nicht geleert werden.
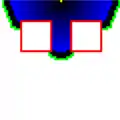 laufende Expandierung
laufende Expandierung abgeschlossene Expandierung
abgeschlossene Expandierung
Eine Blockade tritt auf
Sobald eine Blockade auftritt, werden alle Punkte, die davon betroffen sind, wieder in die OpenList hinzugefügt. Allerdings werden sie als Raise-Punkte markiert (orange Punkte in der Karte). Bevor ein Raise-Punkt jedoch die Kostenerhöhung an seine Folgepunkte weiterreicht, prüft er, ob es in seiner Nachbarschaft einen Punkt gibt, der seine Kosten verringern kann. Nun läuft eine Raise-Welle durch alle betroffenen Punkte. Verfolgt wird diese Welle von einer Lower-Welle (grüne Punkte), insofern es eine solche gibt. Lower-Punkte sind Punkte, die eine Kostenreduktion weiterverbreiten. In diesem Beispiel hat der Punkt ganz rechts die Möglichkeit, über einen alternativen Nachbarn zum Ziel zu führen. Er ist fortan ein Lower-Zustand und zieht sich der Raise-Welle hinterher. Dies ist das Herzstück des D*. Durch diesen Punkt wird verhindert, dass eine ganze Reihe anderer Punkte überhaupt „angefasst“ werden müssen. Es werden nur die Punkte bearbeitet, die auch tatsächlich von der Kostenänderung betroffen sind.
 Blockade eingetragen und betroffene Punkte markiert
Blockade eingetragen und betroffene Punkte markiert laufende Expandierung
laufende Expandierung
Eine weitere Blockade tritt auf
Diesmal lässt sich die Blockade nicht so elegant umgehen. Keiner der Punkte kann über einen Nachbarn eine neue Route zum Ziel finden. Deshalb propagieren sie ihre Kostenerhöhung weiter. Erst außerhalb des Kanals können Punkte gefunden werden, die eine Route zum Ziel zur Verfügung stellen. Hier entstehen zwei Lower-Wellen, die als unerreichbar markierte Punkte mit einer neuen Routeninformation expandieren.
 Durchgang geschlossen
Durchgang geschlossen Expansion
Expansion Neue Route gefunden
Neue Route gefunden
Der Algorithmus
while(openList.nichtLeer())
{
punkt = openList.erstesElement();
expandiere(punkt);
}
Funktion: expandieren
void expandiere(aktuellerPunkt)
{
boolean istRaise = istRaise(aktuellerPunkt);
double kosten;
foreach(nachbar in aktuellerPunkt.getNachbarn())
{
if(istRaise)
{
if(nachbar.nächsterPunkt == aktuellerPunkt)
{
nachbar.setztNächstenPunktUndAktualisiereKosten(aktuellerPunkt);
openList.hinzufüge(nachbar);
}
else
{
kosten = nachbar.berechneKostenÜber(aktuellerPunkt);
if(kosten < nachbar.getKosten())
{
aktuellerPunkt.minimaleKostenAufAktuelleKostenSetzen();
openList.hinzufügen(aktuellerPunkt);
}
}
}
else
{
kosten=nachbar.berechneKostenÜber(aktuellerPunkt);
if(kosten < nachbar.getKosten())
{
nachbar.setztNächstenPunktUndAktualisiereKosten(aktuellerPunkt);
openList.hinzufüge(nachbar);
}
}
}
}
Überprüfung, ob Raise vorliegt
boolean istRaise(punkt)
{
double kosten;
if(punkt.getAktuelleKosten() > punkt.getMinimaleKosten())
{
foreach(nachbar in punkt.getNachbarn())
{
kosten = punkt.berechneKostenÜber(nachbar);
if(kosten < punkt.getAktuelleKosten())
{
punkt.setztNächstenPunktUndAktualisiereKosten(nachbar);
}
}
}
return punkt.getAktuelleKosten() > punkt.getMinimaleKosten();
}
Der Algorithmus in Worten
Alle bekannten Punkte sind auf der OpenList vermerkt. Am Anfang ist das nur der EndPunkt. Solange Punkte auf der OpenList sind, wird immer der erste Punkt aus der OpenList entfernt und expandiert.
Expansion von Punkten
Zuerst wird entschieden, ob der aktuell zu expandierende Punkt im Raise-Zustand ist oder nicht (und damit automatisch im Lower Zustand). Liegt ein Lower-Zustand vor, wird analog zu A* vorgegangen. Alle Nachbarn werden daraufhin untersucht, ob sie vom aktuellen Punkt besser erreicht werden können als bisher. Falls dies der Fall ist, wird der aktuelle Punkt zum Vorgänger des Nachbarn, dessen Kosten neu berechnet und dieser in die OpenList hinzugefügt. Liegt ein Raise-Zustand vor, werden die Kosten sofort an alle Nachbarn weitergereicht, welche über den aktuellen Punkt zum Ziel finden. Für alle anderen Punkte wird geprüft, ob der aktuelle Punkt eine Kostenverringerung darstellen könnte. Falls ja, werden die minimalen Kosten des aktuellen Punktes auf seine aktuellen Kosten gesetzt (er wird somit zum Lower-Zustand) und wieder in die OpenList gesetzt, um bei der nächsten Expansion seine Kostenoptimierung zu propagieren.
Lower/Raise-Entscheidung
Die Entscheidung, ob ein Raise- oder Lowerzustand vorliegt, wird anhand der aktuellen und minimalen Kosten entschieden. Sind die aktuellen Pfadkosten größer als die minimalen, liegt ein Raise-Zustand vor. Bevor diese Kostenerhöhung jedoch weitergegeben wird, wird geprüft, ob es einen Punkt in der Nachbarschaft gibt, welcher die Kosten des aktuellen Punktes senken könnte. Falls es so einen Punkt gibt, wird dieser als neuer Vorgänger gesetzt und die Kosten neu berechnet. Sind alle Nachbarn geprüft worden, wird abermals geprüft, ob die minimalen Kosten den aktuellen Kosten entsprechen. Ist dies der Fall, liegt jetzt ein Lower-Zustand vor, ansonsten bleibt es ein Raise und die Kosten werden propagiert.
Minimale Kosten / aktuelle Kosten
Bei D* ist es wichtig, zwischen aktuellen und minimalen Kosten zu unterscheiden. Erstere interessieren nur zum Zeitpunkt der Erhebung, letztere sind kritisch, denn nach ihnen wird die OpenList sortiert. Die Funktion der minimalen Kosten liefert dabei immer die niedrigsten Kosten, die der Punkt seit seiner ersten "Hinzufügung" auf der OpenList hatte. Beim Hinzufügen einer Blockade ist darauf zu achten, dass diese Funktion einen niedrigeren Wert liefert als die aktuellen Kosten des Punktes.
Optimierung
Der bisher beschriebene D*-Algorithmus funktioniert nicht optimal. Die folgenden Maßnahmen kosten entweder viel Programmieraufwand oder haben nachteilige Effekte, daher ist bei der Implementierung eine Abwägung zu treffen.
Die OpenList
Die Implementierung der OpenList hat die größten Auswirkungen auf die Laufzeit des Algorithmus. Es kann ohne weiteres eine Laufzeit von über 10 sec (einfaches statisches Array) auf unter 100 ms (Balancierter Baum) reduziert werden, sodass sich hier viel Aufwand lohnt. Die Optimierung ist jedoch nicht so einfach wie bei A*. Ein balancierter Baum ist nicht die optimale Lösung, bzw. mit einem normalen balancierten Baum funktioniert D* nicht. Es benötigt mindestens einen balancierten Baum, der damit umgehen kann, dass zwei Objekte den gleichen numerischen Zahlenwert haben, jedoch nicht gleich sind. Zudem muss er in der Lage sein, unter mehreren gleichen Objekten ein spezielles herauszusuchen. Die Standardimplementierungen unter Java oder .NET können das nicht.
Selbst wenn man so einen B-Baum nutzt, ist dies unter Umständen suboptimal. Während der ersten Expansions-Phase treten keine Raise-Zustände auf. Die OpenList wird "im hinteren Drittel" befüllt und von vorne geleert. Der Baum baut sich kontinuierlich auf, bis er seine maximale Größe erreicht hat (die Lower-Welle die größte Ausdehnung besitzt) und anschließend wieder kontinuierlich ab. Bei einer Expandierung einer Blockade kommt es bei Übergängen von Raise- zu Lower-Wellen zu häufigen Änderungen der minimalen Kosten (auf und ab). Damit das Element im Baum gefunden werden kann, muss es entfernt oder anderweitig markiert werden und anschließend wieder eingefügt oder umsortiert werden, was je nach Implementierung und Häufigkeit dieser Änderungen zu einer extremen Verlangsamung führen kann. Unterschiedliche Datenstrukturen für Lower und Raise können hier Abhilfe schaffen oder gleich eine ganz andere Speicher/Zugriffstruktur nutzen.
Punkte überprüfen
Der D*-Algorithmus, wie er hier beschrieben ist, hat ein Problem mit unerreichbar werdenden Punkten. Schließt eine hinzukommende Blockade irgendeinen Bereich vollständig von der Expandierung aus, terminiert er nicht. Das Problem liegt in der Raise-Methode. Vor der Überprüfung, ob ein Raise-Zustand vorliegt, wird versucht, einen Nachbarn zu finden, der günstigere Kosten offeriert. Bei einem Nachbarn einer Blockade ist das jeder Punkt außer die Blockade selbst. Der Raise-Punkt "linkt" sich auf einen Nachbarn, nur um in der nächsten Expandierung durch diesen Nachbarn wieder nach oben gezogen zu werden, um abermals zum Raise-Zustand zu werden. Das endet in einer Schleife, in der die Kosten der Punkte nach oben gezogen werden. Man kann diesem Problem mit zwei Möglichkeiten begegnen:
- fixe Obergrenze: Man richtet eine Obergrenze ein, ab der ein Punkt als "unerreichbar" gilt und keinem Nachbarn als Route zum Ziel dienen darf. So würde die Schleife an dieser Grenze abebben. Diese Methode ist jedoch stümperhaft und die zweite Variante bietet später noch weitere Optimierungs-Möglichkeiten.
- eine Gültigkeitsprüfung: Bevor ein Punkt beim Raise-Check zum Vorgänger gemacht wird, durchläuft er eine Gültigkeitsprüfung. Diese prüft, ob der Punkt in eine Schleife führt, in der OpenList ist, keinen Vorgänger hat (das darf nur der Endpunkt sein), als unerreichbar oder als Blockade markiert ist. Liegt einer dieser vier Fälle vor, wird der Punkt ignoriert. Man kann diese Prüfung von dem gewünschten Punkt bis zum Endpunkt treiben, das kostet jedoch Zeit. Zum Verhindern von Endlosschleifen reicht es jedoch, die nächsten 2 Punkte zu prüfen.
Fokussierende Metrik
Bis jetzt wurde über die verwendete Metrik keine Aussage gemacht. In den Beispielbildern kam eine "Sprung"-Metrik zum Einsatz. Das führt dazu, dass alle Punkte gleich behandelt werden und eine kreisförmige Expansion vorgenommen wird. Eine fokussierende Metrik wäre, wie beim A* für geografische Probleme, die Anzahl der Sprünge vom Punkt bis zum Ziel plus die Luftlinie zwischen dem Punkt und dem Start. Durch diese Metrik wird immer um den zuletzt bekannten optimalen Pfad oder zum Startpunkt hin expandiert. Die Metrik sollte immer schnell zu berechnen sein und muss die tatsächlichen Kosten immer unterschätzen, sonst kommt es zu Fehlern. Im Gegensatz zu A* kann D* durch diese irreparabel beschädigt werden, so dass keine Route zum Ziel gefunden wird.
"Der Fels in der Brandung"
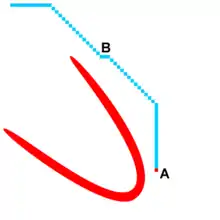
Ein Problem, das mit fokussierenden Metriken jedoch einhergeht, sind spontane Lower/Raise-Wellen im Außenbereich der Karte. Im nebenstehenden Bild ist eine Raisewelle (rot) zu sehen. Diese wird durch die fokussierende Eigenschaft der Metrik stark in eine Richtung gezogen, wodurch ihre seitliche Ausdehnung eher gering ist. Der Punkt A wird als erstes expandiert. Da seine Vorgänger jedoch von der Raise-Welle noch nicht erfasst wurden gilt er als gültig und offeriert seine Kosten. Eine Lower-Welle entsteht. Dieses Phänomen kann nur auftreten, wenn Punkte mit einer hohen Entfernung zum Zielpunkt eher expandiert werden, als Punkte, die dichter am Zielpunkt sind. Ein Punkt, der eigentlich "ungültig" ist oder zumindest später durch eine Raise-Welle geändert wird, wird während eines Raise-Checks als neuer zielführender Nachbar genutzt. Der Raise-Punkt geht infolgedessen in den Lower-Zustand, da er alle Punkte im Umkreis mit seinen Pfadkosten verbessern kann. Nun pulsieren Lower-Wellen gefolgt von Raise-Wellen im Umkreis um diesen Punkt, bis eine finale Lower/Raise-Welle schließlich die korrekten Distanz-Kosten propagiert.
Dieses Problem lässt sich nur bedingt eindämmen. Der Vorteil einer fokussierten Metrik ist zu groß, als dass man sich von solchen "Effekten" im Randbereich stören lässt. Über die Gültigkeitsprüfung ist dem Problem nur bedingt beizukommen. Selbst bei einer Abtastung vom vermuteten Punkt bis zum Zielpunkt kann dennoch eine solche Konstellation zustande kommen. Zudem würde eine solch hohe Abtasttiefe extreme Laufzeiterhöhungen mit sich bringen.
Heuristik: Bei einer N*N-Matrix unterdrückt eine Abtasttiefe von N/20 die meisten dieser Effekte in den ersten 2/3 der zu expandierenden Punkte.
Abbruchbedingungen
Ebenfalls verstärkt wird der Zeitgewinn durch einen verfrühten Abbruch, besonders bei einer fokussierenden Metrik. Wie auch A* kann der Algorithmus abgebrochen werden, sobald der Startpunkt expandiert wird und – das ist D*-spezifisch – dieser im Lower-Zustand ist (gilt nur bei sauberer Implementierung). Bei einem Abbruch darf die OpenList nicht geleert werden, da sonst bei einer auftretenden Blockade nicht alle Wege zu ihrer Umgehung bekannt sind.
Anders als bei A* verschenkt man durch einen verfrühten Abbruch aber auch Potential. D* profitiert davon, so viele Alternativrouten zu kennen wie irgend möglich, um von ebendiesen möglichst schnell wieder einen validen Zustand herbeizuführen. Bricht man jedoch immer ab, sobald man den optimalen Weg gefunden hat, konvergiert D* bei einem Fehlerfall langsamer (aber immer noch schneller als A*).
Multithreading
Die Frage des Abbruches erübrigt sich, sobald man auf eine Multithreading-fähige Plattform zurückgreifen kann. Normalerweise wird der D*-Algorithmus nicht ohne tieferen Sinn programmiert und genutzt (akademische Zwecke ausgenommen). Er dient zur Steuerung von Robotern/Agenten oder ganzen Schwärmen. Üblicherweise braucht es auch seine Zeit, bis diese Geräte hochgefahren sind. Hier setzt das Multithreading an. Der D*-Algorithmus wird als erstes gestartet. Anstatt wie bisher jedoch die Programmausführung zu blockieren, wird die Berechnung in einen einzelnen Thread ausgelagert, dem höchste Priorität zugewiesen wird. Das soll dafür sorgen, dass fast alle anderen Threads blockiert werden und nur noch die Route berechnet wird. Sobald der Algorithmus an den Punkt angelangt ist, an dem man ihn normalerweise terminieren würde (Erstexpansion des Startpunktes) teilt man allen vielleicht wartenden Threads mit, dass die Route nun verfügbar ist. Gleichzeitig nimmt man den Thread von der CPU und reiht ihn wieder ein, diesmal aber mit niedrigster Priorität. So wird jegliche überschüssige Rechenleistung genutzt, um die Karte weiter zu expandieren. In aller Regel reicht die überschüssige Rechenleistung aus, um die Karte vollständig expandiert zu haben, bis der Agent einsatzbereit ist.
Gleiches gilt für das Berechnen von Blockaden. Hier wird der aufrufende Thread solange blockiert, bis der berechnende Thread eine neue Route gefunden hat, anschließend wird die Karte weiter expandiert, während der Agent neue Befehle bekommt.
Weblinks
- Anthony Stentz: Ursprüngliche Publikation. (englisch)