Chomp
Chomp ist ein 2-Personen-Spiel, das mit Papier und Bleistift gespielt werden kann.
Name und Regel
Das Spielfeld ist ein Rechteck, eingeteilt in ein Raster gleich großer Felder. Die Ähnlichkeit mit einer Schokoladentafel hat dem Spiel seinen Namen gegeben, denn das englische Verb to chomp heißt abbeißen. Man kann Chomp gut auf Papier mit Rechenkästchen spielen. Die Spieler entfernen abwechselnd Felder (z. B. durch Markierung der Kästchen) nach der folgenden Regel: Der Spieler am Zug entscheidet sich für eines der noch vorhandenen Felder (Ankerfeld) und entfernt alle noch vorhandenen Felder in demjenigen Rechteck, das das Ankerfeld als linke obere Ecke hat und das unten und rechts bis zum Spielfeldrand reicht. Der Spieler, der das linke obere Feld nehmen muss, verliert das Spiel.
Geschichte
Fred Schuh gilt als Erfinder von Chomp [1]. Er veröffentlichte 1952 das Spel van delers (Spiel der Teiler). Das ist die mehrdimensionale zahlentheoretische Variante von Chomp (siehe Verallgemeinerungen). 1974 folgte durch David Gale die Standardvariante [2], die durch Martin Gardner den Namen Chomp erhielt. Seither sind mehrere Publikationen mit Analysen von Chomp erschienen; eine Gewinnstrategie konnte aber bisher nicht entwickelt werden.
In der deutschen Übersetzung des Standardwerks der mathematischen Spiele Winning Ways von E. R. Berlekamp et al. wurde als Bezeichnung für das Chomp-Spiel Futtern gewählt [3]. Dieser Name scheint sich aber nicht durchgesetzt zu haben.
Beispiel
Das folgende Bild zeigt einen typischen Ablauf beim Chomp-Spiel. Da das Ausgangsrechteck 3 Zeilen und 6 Spalten aufweist, wird dieses Spiel als (3,6)-Chomp bezeichnet. Legale Spielsituationen weisen am unteren Rand der noch vorhandenen Felder eine „Treppe“ von links unten nach rechts oben auf (weiße Felder).
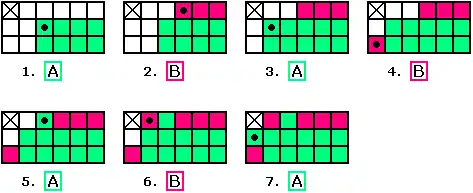
Spieler B muss das letzte Feld (angekreuzt) nehmen und verliert. Die Ankerfelder sind jeweils durch einen Punkt markiert.
Theorie des Spiels
Aus theoretischen Gründen verzichtet man auf die Wegnahme des linken oberen Felds, so dass nicht der Verlierer, sondern der Gewinner den letzten Zug macht; insbesondere soll das Rechteck mehr als ein Feld aufweisen. Mit dieser Vereinbarung lässt sich Chomp innerhalb der Kombinatorischen Spieltheorie als neutrales (oder objektives) 2-Personen-Spiel klassifizieren. Solche Spiele besitzen immer eine Gewinnstrategie für entweder den anziehenden Spieler (1. Zug) oder den nachziehenden Spieler (2. Zug). Das Gleiche gilt für jede denkbare Spielsituation zwischen dem ersten und dem letzten Zug.
Bei Chomp gibt es eine Gewinnstrategie für den anziehenden Spieler. Das weist man mit einem sogenannten Strategiediebstahl nach: Gäbe es eine Gewinnstrategie für den Nachziehenden, so müsste es einen gewinnbringenden Antwortzug auf die Wegnahme des rechten unteren Felds geben. Das Ankerfeld dieses Antwortzugs hätte aber der Anziehende gleich im ersten Zug wählen können; das würde ihm eine Gewinnstrategie verschaffen. Also ist die Annahme einer Gewinnstrategie für den Nachziehenden falsch.
Der Strategiediebstahl ist bei Chomp keine konstruktive Gewinnstrategie. Das bedeutet, dass lediglich die Existenz einer Gewinnstrategie bewiesen wird, aber die Gewinnstrategie selbst daraus nicht abzuleiten ist. Für beliebiges (n,m)-Chomp (d. h. für n Zeilen, m Spalten) ist keine Gewinnstrategie bekannt, wohl aber für kleine Zahlenpaare (n,m), außerdem für alle Zahlenpaare (n,n), (n,2) und (2,m).
Die Gewinnstrategie ist im Allgemeinen nicht eindeutig. Das kleinste bekannte Beispiel, bei dem es mehr als eine Gewinnstrategie gibt, ist (8,10)-Chomp [3].
Verallgemeinerungen der Spielidee
Chomp ist durch das rechteckige, gerasterte Spielfeld einfach darstellbar und spielbar. Es lässt sich allerdings auch zahlentheoretisch statt geometrisch formulieren. Dazu beginnt man mit einer natürlichen Zahl N, die das Produkt zweier Primzahlpotenzen ist: N = pn × qm (p, q verschiedene Primzahlen). Die Spieler wählen abwechselnd als Ankerzahlen Faktoren von N; dabei darf nicht die 1 und kein bereits gewählter Faktor oder ein Vielfaches davon gewählt werden. Der Spieler, für den nur die 1 übrig bleibt, verliert. Dieses Spiel ist spieltheoretisch identisch mit (n+1,m+1)-Chomp, denn das folgende Bild zeigt, dass man alle Faktoren von N in einem (n+1,m+1)-Rechteck anordnen kann; die Ankerzahlen entsprechen dann den Ankerfeldern. Nach Entfernung eines Ankerfelds bleiben nur noch Faktoren übrig, die keine Vielfachen der Ankerzahl sind. Im Bild ist das Ankerfeld in der (i+1)-ten Zeile und der (k+1)-ten Spalte; alle grün umrandeten Felder entfallen. Dann sind nur noch Felder übrig, die keine Vielfachen von pi × qk sind.

Die zahlentheoretische Definition des Chomp-Spiels erlaubt zwei Verallgemeinerungen. Wenn r Primzahlen statt zwei Primzahlen im Produkt für N auftreten dürfen, führen die gleichen Spielregeln zum r-dimensionalen Chomp [3]. Ferner kann man die Beschränkung auf endlich viele Felder aufheben; dann sind als Ankerzahlen alle Produkte der r vorgegebenen Primzahlen mit beliebig hohen Potenzen erlaubt, sofern sie keine bereits gewählten Ankerzahlen oder Vielfache davon sind.
Siehe auch
Einzelnachweise
- Fred Schuh: Spel van delers. Nieuw Tijdschrift voor Wiskunde 39 (1952), S. 299–304
- David Gale: A curious Nim-type game. Amer. Math. Monthly 81 (1974), S. 876–879
- Elwyn R. Berlekamp et al.: Gewinnen - Strategien für mathematische Spiele, Band 3. Vieweg, Braunschweig/Wiesbaden 1986, ISBN 3-528-08533-9, S. 172f