Bogenvieleck
Bogenvielecke oder auch Bogenpolygone sind eine Art von Gleichdicken. Ihnen liegt jeweils ein Vieleck (Polygon) zugrunde, dessen Seiten durch Kreisbögen zwischen jeweils zwei benachbarten Eckpunkten ersetzt werden, deren Mittelpunkt der gegenüberliegende Eckpunkt ist. Das zugrundeliegende Vieleck muss konvex und nicht überschlagen sein und eine ungerade Anzahl an Ecken besitzen.
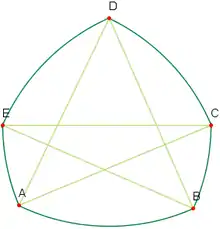

Die regelmäßige Variante, bei der ein regelmäßiges Polygon zugrunde gelegt wird, wird als Reuleaux-Polygon bezeichnet. Sie ist benannt nach dem deutschen Ingenieur und Kinematiker Franz Reuleaux (1829–1905). Die bekannteste Unterform ist das Reuleaux-Dreieck.
Konstruktion
Zur Konstruktion kann das Vieleck vorgegeben werden, dieses muss die Bedingung erfüllen, dass alle Diagonalen gleich lang sind. In diesem Fall ist die Konstruktion recht simpel. Es ist stets um einen Eckpunkt ein Kreisbogen durch die beiden gegenüberliegenden Eckpunkte zu zeichnen.
Doch auch ohne Vorgabe eines Polygons lässt sich ein Bogenvieleck allein mit dem Zirkel konstruieren. Hier am Beispiel des Bogenfünfecks; die Konstruktionsbeschreibung lässt sich jedoch für alle beliebigen Bogenvielecke adaptieren:
- Man lege einen Punkt A fest und zeichne um diesen einen Kreis i.
- Man wähle auf dem Kreis i einen Punkt C und, im mathematisch positiven Sinne weitergehend, einen Punkt D.
- Man zeichne um den Punkt C einen Kreis j durch den Punkt A.
- Man wähle auf dem Kreis j, im mathematisch negativen Sinne von Punkt A weitergehend, einen Punkt E.
- Man zeichne um den Punkt E einen Kreis k durch den Punkt C.
- Man zeichne um den Punkt D einen Kreis l durch den Punkt A. Der Schnittpunkt der Kreis k und l, im mathematisch positiven Sinne von A weitergehend, sei Punkt B.
- Man zeichne um den Punkt B einen Kreis l durch die Punkte D und E.
Es entsteht das Bogenfünfeck ABCDE mit den Kreisbögen AB, BC, CD, DE und EA.
Berechnung des Umfangs
Bei regelmäßigen Bogenfünfecken berechnet sich der Umfang aus der Breite b auf folgende Art und Weise:
Diese Rechnung lässt sich verallgemeinern auf regelmäßige Bogenvielecke beliebiger, ungerader Eckenzahl:
Daraus erkennt man, dass der Umfang beliebiger regelmäßiger Bogenvielecke gleich ist.
Vergleich mit dem Kreis
Der Kreis kann als Grenzfall eines gleichmäßigen Bogenvielecks angesehen werden, dessen Eckenzahl gegen Unendlich geht. Die Breite ist der Durchmesser des Kreises.