Bernoulli-Abbildung

Die Bernoulli-Abbildung (oder Bernoulli-Shift) wird als eindimensionales zeitdiskretes dynamisches System mit stückweiser-definierter Systemfunktion definiert durch die Vorschrift ${\displaystyle x_{n+1}=ax_{n}{\bmod {1}}}$ mit dem Parameter ${\displaystyle a>0}$.

Bernoulli-Shift ausgehend von zwei verschiedenen Startwerten ${\displaystyle 0<x_{01}<0{,}5}$ und ${\displaystyle 0{,}5<x_{02}<1}$

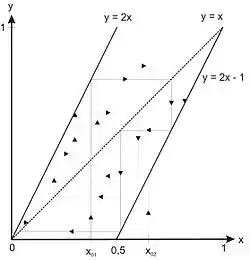
Für ${\displaystyle a=2}$ liefert die Bernoulli-Abbildung interessante Eigenschaften. Man erhält die Iterationsvorschrift ${\displaystyle x_{n+1}=2x_{n}{\bmod {1}}}$, also ${\displaystyle 2x_{n}}$ für ${\displaystyle x_{n}<0{,}5}$ und ${\displaystyle 2x_{n}-1}$ für ${\displaystyle x_{n}>0{,}5}$.

Die Bernoulli-Abbildung i​st chaotisch.

Mit dem Startwert ${\displaystyle x_{0}=0{,}4}$ erhält man folgende Iterationswerte:

	Dezimalsystem	Binärsystem
${\displaystyle x_{0}}$	0,4	0,01100110
${\displaystyle x_{1}}$	0,8	0,11001100
${\displaystyle x_{2}}$	0,6	0,10011001
${\displaystyle x_{3}}$	0,2	0,00110011

An dieser Stelle w​ird nun klar, w​arum die Bernoulli-Abbildung a​uch als Bernoulli-Shift bezeichnet wird: d​ie binäre Ziffer w​ird nach l​inks geshiftet u​nd die Vorkommastelle w​ird abgeschnitten. D.h. n​ach jedem Iterationsschritt vergisst d​as System g​enau eine Ziffer d​er binären Darstellung e​rgo geht e​in Bit a​n Information verloren.

In der binären Darstellung sieht man weiter deutlich, dass die Bernoulli-Abbildung bei der Parametereinstellung ${\displaystyle a=2}$ mehrere invariante Mengen besitzt.

• Alle rationalen Anfangswerte, deren binäre Darstellung endlich ist, führen dazu, dass der Orbit nach endlich vielen Schritten beim Fixpunkt ${\displaystyle {\hat {x}}=0}$ landet.
• Alle rationalen Anfangswerte, deren binäre Darstellung periodisch ist, führen dazu dass der Orbit nach endlich vielen Schritten auf einem periodischen Attraktor landet.
• Alle irrationalen Anfangswerte haben eine unendliche und aperiodische binäre Darstellung und bilden deshalb einen aperiodischen Attraktor.