BFGS-Verfahren

Das Broyden–Fletcher–Goldfarb–Shanno (BFGS) Verfahren i​st ein numerisches Verfahren z​ur Lösung v​on nichtlinearen Optimierungsproblemen. Das Verfahren w​urde von d​en Mathematikern Broyden, Fletcher, Goldfarb u​nd Shanno i​m Jahre 1970 unabhängig voneinander entwickelt u​nd in v​ier wissenschaftlichen Artikeln publiziert.

Beispiellauf des BFGS-Verfahrens mit der Rosenbrock-Funktion ("Bananenfunktion")

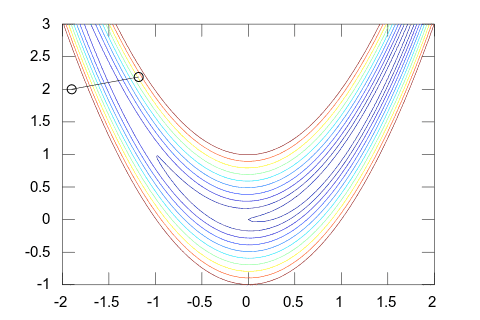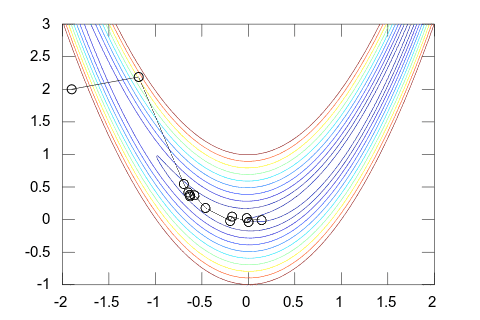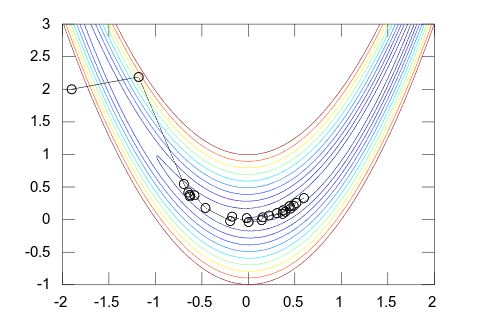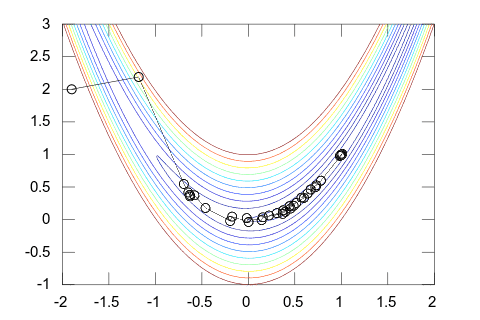
Es gehört z​u der Gruppe d​er Quasi-Newton-Verfahren. Als solches vermeidet e​s die direkte Berechnung d​er Hesse-Matrix, i​ndem es d​ie Hesse-Matrix iterativ approximiert. Bei quadratischen Funktionen benötigen sowohl d​as Newton-Verfahren a​ls auch Quasi-Newton-Verfahren ca. N² Funktionsaufrufe (wenn m​an die Ableitungen über Differenzenquotienten approximiert); d​ies gilt a​uch für d​as Verfahren d​er konjugierten Gradienten. Allerdings h​at sich insbesondere d​as BFGS-Verfahren i​n der Praxis besonders bewährt (z. B. i​st es relativ tolerant gegenüber Fehlern b​ei der Schrittweitensteuerung).

Literatur

• Charles G. Broyden: The convergence of a class of double-rank minimization algorithms. In: Journal of the Institute of Mathematics and Its Applications. Band 6, 1970, S. 76–90, doi:10.1093/imamat/6.1.76.
• Roger Fletcher: A New Approach to Variable Metric Algorithms. In: Computer Journal. Band 13, Nr. 3, 1970, S. 317–322, doi:10.1093/comjnl/13.3.317.
• Donald Goldfarb: A Family of Variable Metric Updates Derived by Variational Means. In: Mathematics of Computation. Band 24, Nr. 109, 1970, S. 23–26, doi:10.1090/S0025-5718-1970-0258249-6.
• David F. Shanno: Conditioning of quasi-Newton methods for function minimization. In: Mathematics of Computation. Band 24, Nr. 111, Juli 1970, S. 647–656, doi:10.1090/S0025-5718-1970-0274029-X.