Asymptotischer Punkt
Ein asymptotischer Punkt einer Kurve ist in der Analysis und der Geometrie – weit gefasst – eine asymptotische Linie, die zu einem Punkt entartet ist[1].
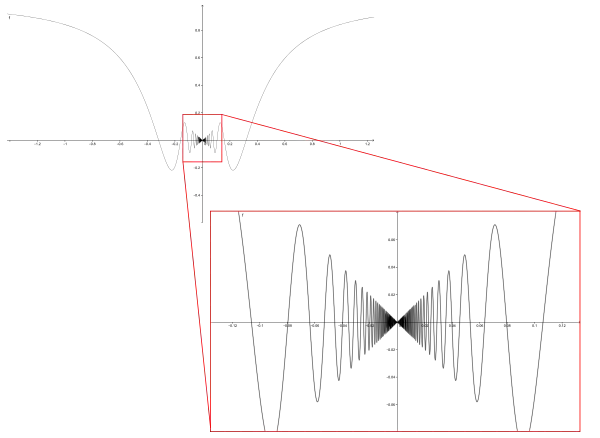
In diesem Sinne kann man einen asymptotischen Punkt als einen Häufungspunkt von Kurvenpunkten auffassen, der selbst kein Kurvenpunkt ist.
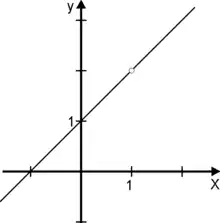
Auch eine stetig behebbare Definitionslücke ist danach ein asymptotischer Punkt.
Oft wird der Begriff aber eingeschränkt auf Punkte, die die Kurve unendlich oft umkreist, ohne sie schließlich zu erreichen. Bei Funktionsgraphen ist dies nicht möglich; typisch für diese Art von asymptotischen Punkten sind Spiralen.
Die logarithmische Spirale hat einen asymptotischen Punkt, die Klothoide zwei.
Eine präzise Definition dieses Begriffs von asymptotischem Punkt ist nicht ganz einfach. Sie läuft darauf hinaus, dass der Tangentenwinkel der Kurve bei Annäherung an den Häufungspunkt dem Grenzwert ±∞ zustrebt.[2]
In dieser Form wird der Begriff auch in der Kugelgeometrie verwendet.
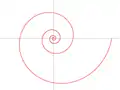 Logarithmische Spirale
Logarithmische Spirale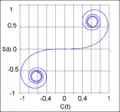 Klothoide
Klothoide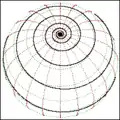
Einzelnachweise
- Lexikon der Mathematik. Heidelberg, Berlin (Spektrum) 2002, Artikel „Asymptote“
- Naas, Schmid: Mathematisches Wörterbuch. Berlin, Stuttgart (Teubner) 1965³