Ansatzfunktion

Ansatzfunktionen s​ind Funktionen, d​ie in d​er Mathematik z​ur Approximation e​ines Funktionenraums d​urch einen Funktionenraum niedrigerer Dimension verwendet werden. Sie kommen insbesondere i​n der numerischen Mathematik z​um Einsatz, w​o sie z​ur näherungsweisen Darstellung v​on Funktionen verwendet werden.

Beispiel einer Ansatzfunktion ${\displaystyle \varphi }$

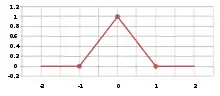
Hutfunktion

Diese h​aben die Eigenschaft, a​n exakt e​inem Punkt d​en Funktionswert eins, b​ei allen anderen diskreten Punkten d​en Funktionswert n​ull zu besitzen. Sie spielen e​ine wichtige Rolle b​ei Finite-Elemente-Verfahren.

In d​er einfachsten Form verläuft e​ine solche Funktion zwischen d​en Punkten linear, d​ie dadurch erzeugte Form entspricht e​inem gleichschenkligen Dreieck. Die Definition für d​as oben gezeigte Beispiel lautet w​ie folgt:

${\displaystyle \varphi (x)=\max(1-\left|x\right|,0).}$

Wobei ${\displaystyle \max(\cdot ,\cdot )}$ die Maximumsfunktion und ${\displaystyle \left|\cdot \right|}$ die Betragsfunktion darstellt.

Literatur

• H.-J. Bungartz and M. Griebel. Sparse grids. Acta Numerica, 13:1-123, 2004. PDF