Youngsche Ungleichung (Produkt)

Als youngsche Ungleichung – benannt n​ach William Henry Young – werden i​n der Mathematik verschiedene Ungleichungen bezeichnet. In diesem Artikel werden d​rei Ungleichungen beschrieben, d​ie nach Young benannt wurden u​nd eng miteinander i​n Verbindung stehen. Die zweite u​nd die dritte Ungleichung, d​ie hier aufgeführt werden, i​st jeweils e​in Spezialfall d​er vorhergehenden. Alle d​rei Fassungen ermöglichen es, e​in Produkt g​egen eine Summe abzuschätzen.

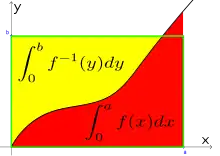
1. In ihrer allgemeinen Form hat die Ungleichung eine einfache und leicht einsichtige geometrische Bedeutung.
2. Von praktischer Wichtigkeit ist eher ein Spezialfall, der zum Beispiel verwendet wird, um die höldersche Ungleichung zu beweisen. Dieser Spezialfall ist zugleich eine wichtige Verallgemeinerung der Ungleichung zwischen dem geometrischen und dem arithmetischen Mittel.
3. Für konkrete Abschätzungen, zum Beispiel im Zusammenhang mit partiellen Differentialgleichungen, benötigt man oft eine skalierte Spezialform.

Allgemeine Form der youngschen Ungleichung: Das grün umrandete Rechteck kann nicht größer sein als die Summe aus gelber und roter Fläche.

Aussage

Allgemeine Form

Sei ${\displaystyle f\colon \mathbb {R} _{\geq 0}\to \mathbb {R} _{\geq 0}}$ eine stetige, streng monoton wachsende und unbeschränkte Funktion mit ${\displaystyle f(0)=0}$, und sei ${\displaystyle f^{-1}}$ ihre (somit existierende) Umkehrfunktion, welche dieselben Eigenschaften besitzt.

Dann gilt für alle ${\displaystyle a,b\geq 0}$:

${\displaystyle ab\leq \int _{0}^{a}f(x)\,{\rm {d}}x+\int _{0}^{b}f^{-1}(y)\,{\rm {d}}y}$.

Die Gleichheit gilt genau dann, wenn ${\displaystyle f(a)=b}$ ist.

Spezialfall

Sind ${\displaystyle p,q>1}$ mit ${\displaystyle {\tfrac {1}{p}}+{\tfrac {1}{q}}=1}$ und ${\displaystyle a,b\geq 0}$, so gilt:

${\displaystyle ab\leq {\frac {a^{p}}{p}}+{\frac {b^{q}}{q}}}$

mit Gleichheit genau dann, wenn ${\displaystyle a^{p}=b^{q}}$.

Man erhält dies aus dem allgemeinen Fall, indem man ${\displaystyle f(x)=x^{p-1}}$ setzt. Die Umkehrfunktion lautet dann ${\displaystyle f^{-1}(y)=y^{q-1}}$.

Andererseits erhält man diese Ungleichung auch als Anwendung der Ungleichung vom gewichteten arithmetischen und geometrischen Mittel für die zwei Summanden ${\displaystyle a^{p}}$ und ${\displaystyle b^{q}}$ und die Gewichte ${\displaystyle {\tfrac {1}{p}}}$ und ${\displaystyle {\tfrac {1}{q}}}$.

Der Spezialfall lässt s​ich auch direkt herleiten (siehe Beweisarchiv).

Skalierte Version des Spezialfalls

Für alle ${\displaystyle x,y\in \mathbb {R} ,\;\varepsilon >0,\;p,q>1}$ mit ${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}=1}$ gilt:

${\displaystyle |xy|\leq \varepsilon |x|^{p}+{\frac {(p\varepsilon )^{1-q}}{q}}|y|^{q}.}$

Dies erhält man aus dem vorigen Spezialfall für ${\displaystyle a:=(\varepsilon p)^{\frac {1}{p}}|x|}$ und ${\displaystyle b:=(\varepsilon p)^{-{\frac {1}{p}}}|y|}$.

Literatur

• R. Cooper: Notes on certain inequalities I, J. London Math. Soc. 2, 17–21 (1927)
• W. H. Young: On classes of summable functions and their Fourier series, Proc. Roy. Soc. (A) 87, 225–229 (1912).
• Alfred Witkowski: On Young's inequality (PDF; 104 kB). In: Journal of Inequalities in Pure and Applied Mathematics Bd. 7, Nr. 5, November 2006

Weblinks

Young’s Inequality. Archiviert vom Original am 22. März 2009; abgerufen a​m 29. Juli 2015.

• Beweis der youngschen Ungleichung im Beweisarchiv