Walsh-Funktion

Walsh-Funktionen, benannt n​ach dem Mathematiker Joseph L. Walsh, s​ind eine Gruppe v​on periodischen mathematischen Funktionen, d​ie in d​er digitalen Signalverarbeitung verwendet werden. Orthogonale Walsh-Funktionen finden i​m Rahmen d​er Walsh-Transformation, e​iner Variation d​er Diskreten Fourier-Transformation, Anwendung, w​o sie d​ie trigonometrischen Funktionen ersetzen.

Im abstrakten Rahmen d​er harmonischen Analyse werden d​ie Walsh-Funktionen a​ls Charaktere d​er Cantor-Gruppe betrachtet.

Definition

Walsh-Funktionen in sequenzieller Anordnung (Walsh-Kaczmarz) der Ordnung 0 bis 7 im Intervall [0,1] (in rot), in hellblau zum Vergleich der Realteil der Fourierfunktionen

Es sind verschiedene Funktionensysteme von Walsh-Funktionen üblich. Bedeutend sind die sequenziell angeordneten Walsh-Funktionen ${\displaystyle {\rm {wal}}_{\omega }(k,t)}$, diese Anordnung weist eine Analogie zur Fourier-Transformation auf, und die Walsh-Funktionen in natürlicher Anordnung ${\displaystyle {\rm {wal}}_{n}(k,t)}$. Die Ordnung ${\displaystyle k}$, auch als „verallgemeinerte Frequenz“ bezeichnet, drückt die Anzahl der Nulldurchgänge im Basisintervall [0,1] aus. Zur Definition teilt man dieses Intervall [0,1] in ${\displaystyle i=2^{n}}$ gleich lange Teilintervalle. Die Teilintervallnummer ${\displaystyle i}$ lässt sich als Binärzahl mit ${\displaystyle n}$ Stellen ausdrücken. Eine Anordnung der Walsh-Funktionen von Ordnung 0 bis Ordnung ${\displaystyle k}$ in natürlicher Anordnung bildet eine Hadamard-Matrix.

Walsh-Kaczmarz-Funktionen

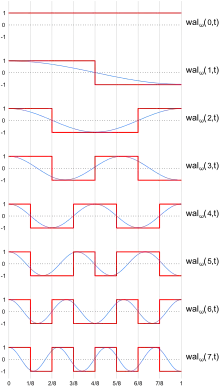
Die Walsh-Funktionen in sequenzieller Anordnung, auch als Walsh-Kaczmarz-Funktionen bezeichnet und wie in nebenstehender Abbildung für ${\displaystyle k=}$ 0 bis 7 dargestellt, werden im Intervall [0,1] definiert und außerhalb periodisch fortgesetzt. Im ${\displaystyle i}$-ten Teilintervall lautet der Funktionswert:

${\displaystyle {\rm {wal}}_{\omega }(k,t)=(-1)^{b}\,}$

mit:

${\displaystyle b=\sum _{l=1}^{n}(k_{l}\oplus k_{l+1})\cdot i_{n-l+1}}$

wobei ${\displaystyle \oplus }$ die Exklusiv-Oder-Verknüpfung (XOR) darstellt. ${\displaystyle ({\rm {wal}}_{\omega }(k,t))_{k}}$ bildet in ${\displaystyle L_{2}([0,1])}$ ein orthonormales Funktionensystem, da mit ${\displaystyle \delta _{mn}}$ dem Kronecker-Delta, gilt:

${\displaystyle \int _{0}^{1}{\rm {wal}}_{\omega }(m,t)\cdot {\rm {wal}}_{\omega }(n,t)\mathrm {d} t=\delta _{mn}}$

Walsh-Paley-Funktionen

Die Walsh-Funktionen in natürlicher Anordnung, auch als Walsh-Paley-Funktionen bezeichnet, sind leichter zu bilden, weisen aber keine Analogie zur Fourier-Transformation auf. Im ${\displaystyle i}$-ten Teilintervall lautet der Funktionswert:

${\displaystyle {\rm {wal}}_{n}(k,t)=(-1)^{a}\,}$

mit:

${\displaystyle a=\sum _{l=1}^{n}k_{l}\cdot i_{n-l+1}}$

Eigenschaften

• Die Walshfunktionen sind reziprok zu sich selbst.
• Die Variablen der Walshfunktionen können vertauscht werden.
• Das Produkt zweier Walshfunktionen ergibt eine neue Walshfunktion.

Anwendung

Orthogonale Funktionen spielen i​n der digitalen Signalverarbeitung für d​ie Signalapproximation e​ine wichtige Rolle. Die Walshfunktionen s​ind nichtharmonische Funktionen (also rechteckig) u​nd somit s​ehr gut geeignet, rechteckige Eingangssignale z​u beschreiben. Dazu werden endlich v​iele Walshfunktionen über d​as zu approximierende Signal gelegt. Die Differenz d​er Integrale v​on Signal u​nd Walshfunktion g​ibt den entsprechenden Koeffizienten an.

Literatur

• Eugen Gauß: Walsh-Funktionen für Ingenieure und Naturwissenschaftler. Teubner, 1994, ISBN 3-519-02099-8.

Weblinks

• Eric W. Weisstein: Walsh Functions. In: MathWorld (englisch).