Ungleichung von Barrow

Die Ungleichung von Barrow, benannt nach David Francis Barrow, ist eine Aussage über Abstände eines Punktes im Inneren eines Dreieckes zu bestimmten Punkten auf dessen Rand. Sie stellt eine Verschärfung der Ungleichung von Erdös-Mordell dar, die besagt, dass die Summe der Abstände von den Ecken immer mindestens doppelt so groß ist wie die Summe der Abstände von den Seiten.

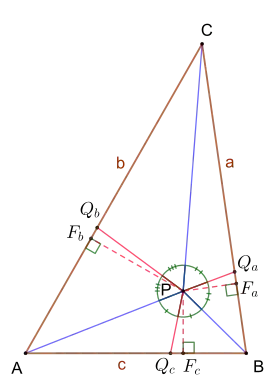
Barrow als Verschärfung von Erdös-Mordell

{\begin{aligned}&\quad \,|PA|+|PB|+|PC|\\&\geq 2(|PQ_{a}|+|PQ_{b}|+|PQ_{c}|)\\&\geq 2(|PF_{a}|+|PF_{b}|+|PF_{c}|)\end{aligned}}

Ungleichung

Gegeben ist ein beliebiger Punkt $P$ im Inneren eines Dreiecks $\triangle ABC$ . Die Winkelhalbierenden der Winkel $\angle APB$ , $\angle BPC$ und $\angle CPA$ schneiden die Dreiecksseiten $a,b,c$ in den Punkten $Q_{a},Q_{b},Q_{c}$ . Es gilt dann die folgende Ungleichung:[1]

|PA|+|PB|+|PC|\geq 2(|PQ_{a}|+|PQ_{b}|+|PQ_{c}|)

.

Barrow veröffentlichte 1937 einen Beweis zur Ungleichung von Erdös-Mordell, der die später nach ihm benannte Ungleichung als Zwischenschritt enthielt.[1]

Verallgemeinerung

Die Ungleichung von Barrow kann auf konvexe Polygone verallgemeinert werden. Für ein konvexes Polygon mit Eckpunkten $A_{1},A_{2},\ldots ,A_{n}$ und einem Punkt $P$ in seinem Inneren bezeichne $Q_{1},Q_{2},\ldots ,Q_{n}$ die Punkte die beim Schnitt mit den Winkelhalbierenden der Winkel $\angle A_{1}PA_{2},\ldots ,\angle A_{n-1}PA_{n},\angle A_{n}PA_{1}$ mit Polygonseiten $A_{1}A_{2},\ldots ,A_{n-1}A_{n},A_{n}A_{1}$ entstehen. Es gilt dann die folgende Ungleichung:[2][3]

\sum _{k=1}^{n}|PA_{k}|\geq \sec \left({\frac {\pi }{n}}\right)\sum _{k=1}^{n}|PQ_{k}|

.

Hierbei bezeichnet $\sec$ die Sekansfunktion und im Fall $n=3$ erhält man wegen $\sec \left({\tfrac {\pi }{3}}\right)=2$ genau die Ungleichung von Barrow.

Literatur

Jian Liu: Sharpened versions of the Erdös-Mordell inequality. In: Journal of Inequalities and Applications, Ausgabe 1, 2015
Alexander Ostermann, Gerhard Wanner: Geometry by its History. Springer, 2012, ISBN 978-3-642-29163-0, S. 222–224
Branko Malesevic, Maja Petrovic: Barrow's Inequality and Signed Angle Bisectors. In: Journal of Mathematical Inequalities, Band 8, Nr. 3, 2014
Paul Erdös, L. J. Mordell, David F. Barrow: Solution to 3740. In: The American Mathematical Monthly, Band 44, Nr. 4 (April, 1937), S. 252–254 (JSTOR)

Einzelnachweise

Alexander Ostermann, Gerhard Wanner: Geometry by its History. Springer, 2012, ISBN 978-3-642-29163-0, S. 222–224
M. Dinca: A Simple Proof of the Erdös-Mordell Inequality. In: Articole si Note Matematice, 2009
Hans-Christof Lenhard: Verallgemeinerung und Verschärfung der Erdös-Mordellschen Ungleichung für Polygone. In: Archiv für Mathematische Logik und Grundlagenforschung, Band 12, S. 311–314, doi:10.1007/BF01650566, MR 0133060.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[OW-1] Alexander Ostermann, Gerhard Wanner: Geometry by its History. Springer, 2012, ISBN 978-3-642-29163-0, S. 222–224

[2] M. Dinca: A Simple Proof of the Erdös-Mordell Inequality. In: Articole si Note Matematice, 2009

[3] Hans-Christof Lenhard: Verallgemeinerung und Verschärfung der Erdös-Mordellschen Ungleichung für Polygone. In: Archiv für Mathematische Logik und Grundlagenforschung, Band 12, S. 311–314, doi:10.1007/BF01650566, MR 0133060.