Triangulatur
Die Triangulatur („dreieckig machen“, von lat. Triangulum, „Dreieck“), auch Triangulation, war eine historische Methode zur Bestimmung von Proportionen von Bauwerken, dem innewohnenden Verhältnis der Längen-, Breiten- und Höhenmaße eines Bauwerks, einer Fassade oder eines Bauteils zueinander, wurde in der Romanik bis zum heutigen Tage angenommen.
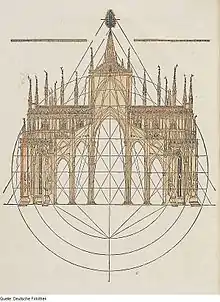
Triangulatur
Die Triangulatur soll vor allem von den Baumeistern zumeist unter Anwendung eines gleichschenkeligen Dreiecks zu Bauwerkskonstruktionen in der Romanik und Gotik verwendet worden sein. Dabei soll die Festlegung bzw. Konstruktion eines Baus oder einzelner seiner Teile mit Hilfe von Seilen, Richtscheit und Zirkel erfolgt sein.
In der einfachsten Form soll dieses Verfahren folgendermaßen angewendet worden sein: Um die Breite und Höhe eines Bauwerks festzulegen, wurde zunächst die Breite durch die Punkte A und B festgelegt. Diese Strecke ist als Schenkel definiert und wenn die identisch lange Strecke AB vom Punkt A und B zu einem Punkt C verbunden wird, entsteht ein gleichschenkeliges Dreieck. Die Senkrechte auf der Streckenhalbierende AB ist zum einen die halbe Länge des Bauwerks und zum anderen das Höhenmaß des Baus. Wird parallel zu AB durch C eine Strecke verschoben, ergibt sich die Strecke DE, die das gleiche Längenmaß von AB hat. Bei einer dreischiffigen Basilika haben die Seitenschiffe die viertel Länge und das Hauptschiff die halbe Länge von AB. Wird der Punkt D und E mit der Mitte von AB verbunden, entstehen Schnittpunkte, das die Länge des Bauwerks vierteln. Dieses einfache Verfahren nennt man Triangulatur. Es sind elf Methoden der Triangulatur bekannt.
Konrad Hecht überprüfte mit elf Methoden der Triangulatur die Proportionierung des Freiburger Münsters und kam zu dem Ergebnis, dass sich die Baumeister der Gotik nicht an den Proportionsfiguren der Triangulatur orientiert haben. „Der gotische Architekt kannte weder "Zaubermittel" noch "Schönheitserzeuger". An der Baustelle wie am Reißbrett benutzte er als einzig verlässliche Hilfsquelle Maß und Zahl; zu allem, was er schuf, zu allem, was uns als Leistung der Gotik heute noch angeht, waren ihm diese Hilfsmittel unentbehrlich“.[1]
Albrecht Kottmann widerspricht Hecht deutlich und kommt zum gegenteiligen Ergebnis. Er belegt eindeutig die Anwendung der Triangulatur beim Freiburger Münster[2].
Es wurde des Weiteren angenommen, dass die Proportionierung von Fialen, Wimpergen, Kreuzblumen und Giebeln entweder mittels Quadratur oder Triangulatur erfolgte.
Als das Büchlein von der Fialen Gerechtigkeit von Matthäus Roritzer (1486), der Dombaumeister in Regensburg war, wiederentdeckt wurde, wurde in der Romantik angenommen, dass die Steinmetzen in der Gotik in der Lage waren, anhand der Maßverhältnisse des Dombaus jederzeit die Maße aller anderer Bausteine zu bestimmen, die sie anzufertigen hatten. Auch diese Auffassung widerlegte Hecht: „Die Bildquellen zeigen keine Proportionsfiguren. Sie zeigen das Abschnüren von Fluchten [..]. Die italienischen Quellen hatten keine historische Grundlage gegeben. Mit den deutschen und mit den französischen Quellen steht es nicht anders.“[3]
Literatur
- Alhardt von Drach: Das Hütten-Geheimnis von grechten Steinmetzen – Grund in seiner Entwicklung und Bedeutung für die kirchliche Baukunst des deutschen Mittelalters, dargelegt durch Triangulatur-Studien an Denkmälern aus Hessen und Nachbargebieten, Marburg 1897.
- Albrecht Kottmann: Fünftausend Jahre messen und bauen. Planungsverfahren und Maßeinheiten von der Vorzeit bis zum Ende des Barock, Julius Hoffmann Stuttgart 1981; ISBN 3 87346 065 3.
- Karl Birker: Der geometrische Aufbau der Ostseite des Gewandhauses in Braunschweig. Versuch einer Deutung, Braunschweig 1984.
- Konrad Hecht: Maß und Zahl der gotischen Baukunst. 3 Teile in 1 Band (Nachdruck der Ausgabe Göttingen 1967–72), Olms Hildesheim, Zürich, New York 1997.
- Theodor Fischer: Zwei Vorträge über Proportionen, Oldenbourg 1956.
- Lexikon der Kunst, Architektur, Bildende Kunst, Angewandte Kunst, Industriegestaltung, Kunsttheorie. Band V, S. 217, hrsg. v. Ludger Alscher, Günter Feist, Peter H. Feist, Verlag Das europäische Buch, Westberlin 1984.
Siehe auch
Einzelnachweise
- Konrad Hecht, Maß und Zahl, S. 469f
- Albrecht Kottmann, Fünftausend Jahre messen und bauen, Planugsverfahren und Maßeiheitenn von der Vorzeit bis zum Ende des Barock, Julius Hoffmann Verlag Stuttgart, 1981, Freiburger Münster auf Seiten 96 bis 100
- Konrad Hecht, Maß und Zahl, S. 223 (siehe Literatur)