Tennis (Bleistiftspiel)

Tennis ist ein strategisches Papier-und-Bleistift-Spiel für zwei Spieler.

Regeln

Das Spielfeld besteht aus 7 Feldern, die mit den Zahlen −3 bis +3 bezeichnet sind. Der Ball liegt zu Beginn auf Feld 0. Jeder Spieler hat ein Punktekonto mit anfänglich z. B. 50 Punkten. Spieler Plus versucht, den Ball auf Feld 3, und Spieler Minus, ihn auf Feld −3 zu schlagen.

In jedem Zug wählen die Spieler gleichzeitig eine natürliche Zahl, die nicht größer sein darf als ihr jeweiliger Punktestand. Hat man noch nicht alle Punkte aufgebraucht, muss man eine positive Zahl wählen. Wer die höhere Zahl nennt, schlägt damit den Ball auf die gegnerische Seite oder, falls er schon dort ist, noch ein Feld weiter. Nennt etwa Spieler Plus die höhere Zahl, dann wird der Ball auf das nächsthöhere Feld, mindestens aber auf Feld 1 geschlagen. Gelangt der Ball dadurch auf Feld 3, gewinnt Spieler Plus. Für Spieler Minus gilt das entsprechende in Gegenrichtung. Wählen beide die gleiche Zahl, ändert sich die Ballposition nicht. Die von jedem Spieler gewählte Zahl wird von dessen Punktestand abgezogen, bevor der nächste Zug gespielt wird.

Das Spiel endet auch dann, wenn kein Spieler mehr Punkte hat. Dann gewinnt Plus, wenn der Ball auf einem positiven, und Minus, wenn er auf einem negativen Feld liegt. Liegt er auf dem Feld 0 (was nur passiert, wenn beide in jedem Zug die gleiche Zahl wählen), endet das Spiel unentschieden.

Wenn man mehrfach spielt (bis eine bestimmte Punktgrenze erreicht wurde), kann man festlegen, dass für das Herausschlagen über die Grundlinie (Ball auf Feld 3 oder −3) 2 Gewinnpunkte vergeben werden, sonst nur 1 Gewinnpunkt.

Mathematische Beschreibung

Zu Beginn ist die Ballposition $B_{0}=0$ und die Spieler $i\in \{1,2\}$ haben den Punktestand $S_{i,0}=50$ . Spieler 1 entspricht Spieler Plus.

In Zug $t\in \mathbb {N} ^{+}$ wählt jeder Spieler als seinen Zug eine ganze Zahl $Z_{i,t}$ mit $\min(1,S_{i,t-1})\leq Z_{i,t}\leq S_{i,t-1}$ . Die gewählte Zahl reduziert die Punkte des Spielers: $S_{i,t}=S_{i,t-1}-Z_{i,t}$ . Für die neue Ballposition gilt:

$B_{t}={\begin{cases}\max(1,B_{t-1}+1)&{\text{wenn}}\;Z_{1,t}>Z_{2,t}\\B_{t-1}&{\text{wenn}}\;Z_{1,t}=Z_{2,t}\\\min(-1,B_{t-1}-1)&{\text{wenn}}\;Z_{1,t}<Z_{2,t}\end{cases}}$

Das Spiel endet, sobald $B_{t}<-2$ oder $B_{t}>2$ oder $S_{1,t}=S_{2,t}=0$ . Wenn $B_{t}>0$ , dann gewinnt Spieler 1, und wenn $B_{t}<0$ , dann gewinnt Spieler 2, und im Fall $B_{t}=0$ endet das Spiel unentschieden.

Beispiel-Spiele

Spielverlauf nach Tabelle 1

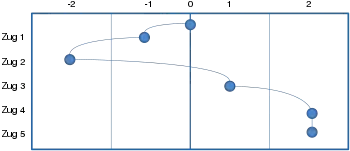
Im ersten Beispiel gewinnt Spieler 1, nachdem beide Spieler keine Punkte mehr haben (Ball noch im Feld).

t	Spieler 1 Zug $S_{1,t}$	Spieler 2 Zug $S_{2,t}$	Spieler 1 Status $Z_{1,t}$	Spieler 2 Status $Z_{2,t}$	Ballort $B_{t}$	Kommentar
0			50	50	0	Start
1	5	10	45	40	−1
2	5	10	40	30	−2
3	15	10	25	20	1
4	15	10	10	10	2
5	10	10	0	0	2	Spieler 1 gewinnt

Spielverlauf nach Tabelle 2

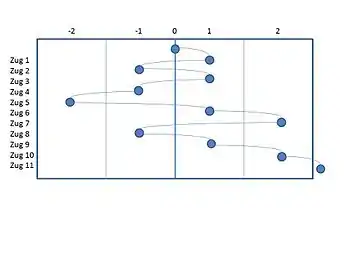
Im zweiten Beispiel gewinnt Spieler 1, indem er mit seinen letzten Punkten den Ball über die Grundlinie hinaus schlagen kann.

t	Spieler 1 Zug $S_{1,t}$	Spieler 2 Zug $S_{2,t}$	Spieler 1 Status $Z_{1,t}$	Spieler 2 Status $Z_{2,t}$	Ballort $B_{t}$	Kommentar
0			50	50	0	Start
1	11	3	39	47	1
2	1	10	38	37	−1
3	15	11	23	26	1
4	1	9	22	17	−1
5	3	6	19	11	−2
6	11	3	8	8	1
7	4	3	4	5	2
8	1	5	3	0	−1
9	1	0	2	0	1
10	1	0	1	0	2
11	1	0	0	0	3	Spieler 1 gewinnt

Spieltheoretische Untersuchung

Der Reiz des Spiels besteht darin, dass die Wahl eines hohen Zuges zwar den Ball auf die Seite des Gegners bringt, aber gleichzeitig weniger Punkte als beim Gegner für die kommenden Züge verbleiben. Eine gute "Strategie" wird versuchen, eine eigene positive Differenz gering zu halten, doch eine negative Differenz eher hoch, um sowohl beim Ballort als auch bei den verbleibenden Punkten in Vorteil zu kommen.

Die Endphase des Spiels kann für $S_{1,t}\leq 3$ und $S_{2,t}\leq 3$ einer der Spieler immer den Sieg erzwingen (deterministisch). Schon für $S_{1,t}=S_{2,t}=4$ und $|B_{1,t}|=1$ gibt es jedoch mehrere Spielausgänge, so dass die Spielstrategie nur auf die Erhöhung der Gewinnwahrscheinlichkeit ausgerichtet sein kann. Für die Analyse des Spiels ist wichtig, dass die Gewinnwahrscheinlichkeit nur von der Anzahl der Punkte beider Mitspieler und dem Ballort abhängt (Zustand des Spiels), nicht jedoch von der Anzahl der Züge die zu diesem Zustand führten oder auf welchem Weg dieser Zustand erreicht wurde (Markow-Eigenschaft).

Technische Implementierung

Das Spiel ist für eine programmtechnische Implementation geeignet, bei der das Programm aus dem Spielen lernt. Der Zustandsraum ist bei einem Startwert von 50 auf 13005 (=51 * 51 * 5, Punktmöglichkeiten der Spieler inkl. 0 sowie 5 Ballorte) begrenzt, und die Spielmatrix sind die möglichen Züge $0\leq Z_{i}\leq S_{i}$ vs. die Zustände ( $S_{1},S_{2},B$ ), sie hat ca. 330000 Elemente, wenn man die nicht erlaubten Züge nicht aufnimmt.

Wenn ein Zug im Endergebnis zum Gewinn führt, wird er aufgewertet, sonst abgewertet. Je höher die Wertung eines Zuges zu einem gegebenen Zustand ist, desto größer soll die Wahrscheinlichkeit sein, dass dieser beim nächsten Erreichen dieses Zustandes gewählt wird. Man kann ein solches Programm gegen sich selbst spielen lassen, wobei bereits 100.000 Spiele zu Strategien führen, die gegen menschliche Gegner fast 50 % Gewinnwahrscheinlichkeit erreichen.

Varianten

Das Spiel wird anspruchsvoller, wenn die gewählten Zahlen nur einem Spielleiter mitgeteilt werden, der den Ballort nach dem Zug bekannt gibt. In diesem Fall ist die Punktdifferenz zum Gegner – und damit auch der aktuelle Punktestand des Gegners – nicht bekannt. Insbesondere gilt für diese Variante nicht mehr die Markow-Eigenschaft, so dass auch eine programmtechnische Implementierung komplexer wird.

Literatur

Matthias Mala: Das große Buch der Block- und Bleistiftspiele, Tosa Verlag, 2005, ISBN 3-85492-542-5.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.