Taylor-Kreis

Der Taylor-Kreis eines Dreiecks ist einer der besonderen Kreise der Dreiecksgeometrie.

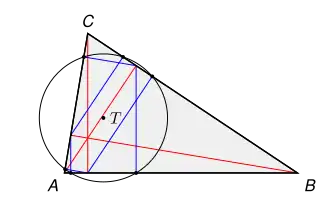
Grafische Darstellung des Taylor-Kreises

Der Taylor-Kreis ist nach Henry Martin Taylor (1842–1927) benannt.

Um den Taylor-Kreis zu erhalten, muss man zunächst die Höhen, also die Lote von den Ecken des Dreiecks auf die gegenüber liegenden Seiten zeichnen. Anschließend werden von jedem der drei Höhenfußpunkte je zwei Lote auf die beiden Nachbarseiten gefällt. Diese sechs Lote werden auch als die Nebenhöhen des Dreiecks bezeichnet. Es kann bewiesen werden, dass die sechs Fußpunkte der Nebenhöhen auf einem Kreis liegen. Um den Mittelpunkt dieses so genannten Taylor-Kreises zu finden, braucht man nur zwei Mittelsenkrechte für je zwei der sechs erwähnten Fußpunkte zum Schnitt zu bringen.

Radius

Der Radius des Taylor-Kreises ist

R_{T}=R{\sqrt {\sin ^{2}\alpha \sin ^{2}\beta \sin ^{2}\gamma +\cos ^{2}\alpha \cos ^{2}\beta \cos ^{2}\gamma }},

wobei R der Umkreisradius ist.

Mittelpunkt

Der Mittelpunkt des Taylor-Kreises hat die baryzentrischen Koordinaten

${\Big (}\sin \alpha [\cos \alpha -\cos(2\alpha )\cos(\beta -\gamma )]:\sin \beta [\cos \beta -\cos(2\beta )\cos(\gamma -\alpha )]:\sin \gamma [\cos \gamma -\cos(2\gamma )\cos(\alpha -\beta )]{\Big )}$

und liegt auf der Brocard-Achse. Er hat die Kimberling-Nummer $X(389).$

Weblinks

Eric W. Weisstein: Taylor Circle. In: MathWorld (englisch).
Taylor-Kreis – eine Visualisierung mit GeoGebra

Siehe auch

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.