Sprouts
Sprouts (engl. Sämlinge) ist der Name eines 1967 von den Mathematikern John Horton Conway und Michael S. Paterson erfundenen Spiels für zwei Spieler. Beide Spieler verbinden auf einem Blatt Papier Punkte mit Linien. Es gewinnt, wer die letzte Linie setzt. Neben dem Zeitvertreib ist das Spiel eine gute Einführung in die Topologie. Ein anderer Name für das Spiel ist Peruanischer Maulwurf (engl.: Peruvian mole).
| Sprouts | |
| Art | Papier- und Bleistiftspiel |
| Kommerz. | Freies Spiel |
| Jahr | 1967 |
| Autor | John Horton Conway |
| # Spieler | 2 |
| Alter | unbegrenzt |
| Dauer | 2–10 Minuten |
| Alles über Spiele: Portal:Spiele | |
Der Zusammenhang mit der Topologie besteht darin, dass alle Sprouts-Partien unter Homöomorphismen invariant sind: Eine Sprouts-Partie kann man auf ein Gummituch aufmalen und dann das Gummituch beliebig verzerren. Durch diese Verformung bleiben dennoch alle wesentlichen Merkmale der Partie erhalten, insbesondere, wer die Partie gewinnt.
Geschichte
Sprouts wurde 1967 von den Mathematikstudenten John Conway und Michael Paterson auf der Universität Princeton als Zeitvertreib erfunden. Laut Conway verteilt sich der Anteil der beiden Erfinder im Verhältnis 2/5 (Conway) zu 3/5 (Paterson), denn Paterson habe die Idee gehabt, auf die neu eingezeichneten Linien einen neuen Punkt zu malen. Den Namen erhielt es durch seine baldige, rege Verbreitung auf dem Campus, die an die essbaren Sprossen erinnerte – es „spross“ sprichwörtlich überall und innerhalb kurzer Zeit entstanden eine ganze Zahl von Varianten und Lösungsvorschlägen.
Regeln
In der Originalversion, Princeton sprouts, wird mit einer beliebigen Anzahl von Punkten auf dem Papier begonnen – je mehr, desto komplexer und länger wird das Spiel. Abwechselnd zeichnet jeder Spieler eine Linie, die in einem Punkt beginnt und in einem Punkt endet (einem anderen, oder auch als Schleife in demselben). Auf die Verbindungslinie zeichnet er einen neuen Punkt ein. Die Linie darf keine vorhandenen Linien oder andere Punkte berühren oder kreuzen. In jedem Punkt dürfen höchstens drei Enden einer Linie vorhanden sein (wenn es eine Schleife ist, zählt sie als zwei Enden). Wer als letztes eine Linie zeichnen kann, gewinnt.
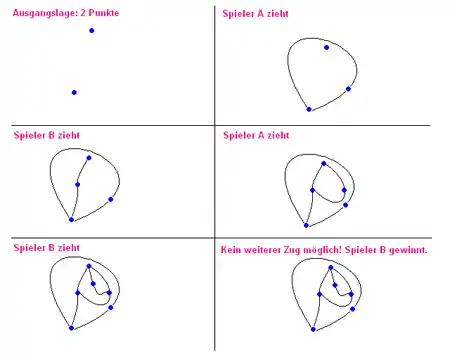
Analyse
Obwohl sich das Spiel recht einfach anhört, entwickelt jeder Spieler nach den ersten Partien bereits ein Gespür für seine Komplexität. Die Länge eines Spiels ist jedoch stets begrenzt, wie sich leicht zeigen lässt:
Wir betrachten ein Spiel mit n Startpunkten, welches m Züge dauert. Am Anfang hat jeder Punkt 3 Leben, denn es können maximal drei Linien von ihm ausgehen. Das Spiel beginnt also mit 3n Leben. Jeder Zug verbraucht 2 Leben (am Anfang- und Endpunkt der Linie) und bringt ein neues (der neue eingezeichnete Punkt hat genau ein freies Leben), reduziert die Anzahl der Leben daher um eins. Da beim letzten Zug immer noch ein freies Leben entsteht (beim letzten eingezeichneten Zug), gilt: 3n − m ≥ 1, oder andersherum: m ≤ 3n − 1.
Das Spiel ist daher spätestens nach 3n − 1 Zügen zu Ende.
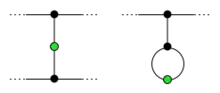
Am Ende des Spieles hat jeder noch lebende Punkt genau zwei tote Nachbarn (siehe Diagramm links). Ein toter Punkt hat immer drei Nachbarn, von welchen einer oder auch keiner ein Überlebender sein kann: kein toter Punkt kann der Nachbar von zwei oder gar drei verschiedenen Überlebenden sein, andernfalls gäbe es ja einen Zug, der zwei der Überlebenden verbände. Alle toten Punkte, die keine überlebenden Nachbarn haben, heißen Pharisäer (hebräisch für die Abgeschiedenen).
Es gilt also:
- n + m = 3n − m + 2(3n − m) + p
denn n + m ist die Gesamtzahl der Punkte am Ende (anfängliche Punkte + Anzahl der Züge, bei jedem Zug kommt ein Punkt hinzu), diese wiederum ergibt sich aus Anzahl der Überlebenden (3n − m) plus Anzahl der Nachbarn 2(3n − m) plus Anzahl der Pharisäer (p). Durch Umstellen und Zusammenfassen erhält man:
- m = 2n + p/4
Also dauert ein Spiel mindestens 2n Züge, und die Zahl der Pharisäer ist immer durch 4 teilbar.
Notation
Die offizielle Notation der WGOSA, die sog. Conway-Notation, entstand etwa 1999 in einem Diskussionsforum.[1] Diese Version wurde längere Zeit akzeptiert, bis Dan Hoey herausfand, dass sie nicht alle Partien eindeutig beschreiben kann. Hoey entwickelte daraufhin eine eigene Notation, während die Standardnotation ergänzt wurde[2].
Die Standardnotation beginnt mit der Anzahl der Startpunkte, und es folgt ein „+“ für eine Normalpartie oder ein „−“ für eine Misère-Partie, siehe unten. Anschließend werden die Namen der Spieler in Klammern aufgeführt, zuerst der Spieler, der den ersten Zug hat, dann der zweite Spieler. Der einladende Spieler wird mit einem Stern „*“ markiert.
- Beispiel: 3+ (Müller, Schmitz*) ist eine normale 3-Punkt-Partie zwischen Müller und Schmitz, Schmitz hat eingeladen, Müller am Zug.
In der Standardnotation werden zunächst die Startpunkte in der Reihenfolge ihrer Verwendung durchnummeriert, neue Punkte erhalten fortlaufende Nummern, so wie sie entstehen. Jeder Zug besteht mindestens aus einem Zahlentripel der Form f(g)h, wobei f und h die Endpunkte der Linie markieren und g den neu eingezeichneten Punkt. Wenn bei einem Zug eine neue Region entsteht, werden die Punkte, die durch diesen Zug von allen übrigen getrennt werden, in eckigen Klammern aufgeführt.
- Beispiel: 1(10)3 [2, 5, 7–9] ist ein Zug von 1 nach 3, Punkt 10 neu erzeugt, die Punkte 2, 5 und 7 bis 9 werden von den übrigen abgetrennt.
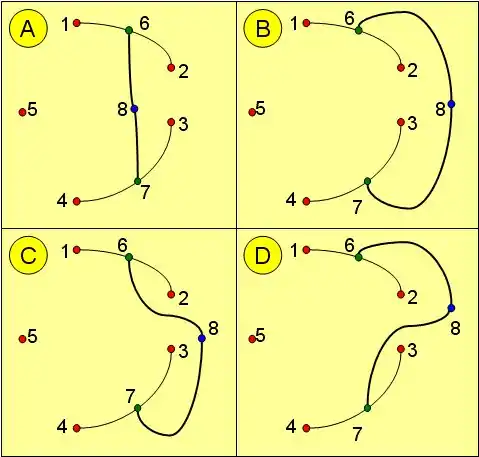
Wie man auf dem nebenstehenden Bild sieht, gibt es in bestimmten Situationen mindestens zwei (topologisch verschiedene) Möglichkeiten, zwei Punkte zu verbinden.
- Beispiel: Die Illustration zeigt ein 5-Punkte-Spiel, bisher wurde gezogen 1(6)2 3(7)4. Für den folgenden Zug 6(8)7 gibt es vier topologisch verschiedene Zugmöglichkeiten.
Zur Unterscheidung der vier Zugmöglichkeiten verwendet man das sog. Hoey-Exclam, ein Ausrufezeichen, das zur Unterscheidung eingesetzt wird. Um die Funktionsweise des Hoey-Exclams zu verstehen, denke man sich eine Ameise, die von Punkt 8 ausgehend in Richtung der Punkte 6 oder 7 krabbelt. Am Punkt 6 oder 7 angekommen, sieht sie die Nachbarn dieser Punkte. Entweder ist der Punkt mit der höheren Nummer rechts oder links. Wenn der Punkt mit der höheren Nummer links ist, wird das Hoey-Exclam eingesetzt.
- Beispiel: Die Varianten A bis D werden folgendermaßen notiert:
- A: 1(6)2 3(7)4 6(8)7
- B: 1(6)2 3(7)4 6!(8)!7
- C: 1(6)2 3(7)4 6(8)!7
- D: 1(6)2 3(7)4 6!(8)7
Wer gewinnt?
Durch vollständige Analyse aller möglichen Spielverläufe kann man zeigen, dass der erste Spieler ein Spiel mit 3, 4 oder 5 Punkten gewinnen kann. Der zweite Spieler kann jedes Spiel mit einem, zwei oder sechs Punkten gewinnen.
David Applegate, Guy Jacobson und Daniel Sleator von den Bell Labs lösten 1990 alle Spiele mit maximal 11 Punkten. Sie fanden, dass der erste Spieler eine Gewinnstrategie hat, wenn die Zahl der Punkte beim Teilen durch 6 einen Rest von 3, 4 oder 5 ergibt. Eine tiefergehende Analyse aus dem Jahr 2007 zeigt, dass dies für alle Spiele mit bis zu 32 Punkten zutrifft[3]. Es wird angenommen, dass die erwähnte Regel für jede Anzahl von Punkten gilt.
Varianten
Sprouts kann misère gespielt werden – dabei verliert im Gegensatz zu dem normalen Sprouts der Spieler, der die letzte Linie zieht. Im Vergleich zum Original erweist sich Misère Sprouts als schwieriger zu analysieren. Die gegenwärtige Vermutung ist, dass der Spieler mit dem ersten Zug gewinnt, wenn die Anzahl der Punkte geteilt durch 6 den Rest 0, 4 und 5 ergibt – wobei die Spiele für eine Punktzahl von 1 oder 4 eine Ausnahme von dieser Regel bilden[4].
Beim Black-and-white sprouts hat der ziehende Spieler die Wahl, ob er auf seine gerade gezogene Linie einen Punkt setzt oder nicht. Diese Version ist gelöst, es gewinnt bei perfektem Spiel der beginnende Spieler.[5] Beim Brussels sprouts (scherzhaft nach der englischen Übersetzung für Rosenkohl benannt) spielt man nicht mit Punkten, sondern mit Kreuzen, deren vier Arme zu verbinden sind. Jeder Punkt hat also vier „Leben“, doch sind die Linien vorgegeben. Diese Version ist wesentlich einfacher als die Originalversion, gelöst und nur als Spaß gedacht. Jedes Spiel dauert 5n-2 Züge.
Beim Antwerp sprouts wird das Spiel zusätzlich mit Farben gespielt.
Literatur
Martin Gardner: Mathematical Carnival. Penguin, 1976 (dt. Mathematischer Karneval. Ullstein, 1977)
Einzelnachweise
- Topic: Sprouts Notation (Memento vom 6. März 2010 auf WebCite) auf The Math Forum@Drexel (im WebCite-Archiv)
- Beitrag von Danny Purvis in der Newsgroup geometry.research
- Lemoine, Viennot, A further computer analysis of Sprouts (PDF; 180 kB), 2007
- Julien Lemoine, Simon Viennot, Analysis of misere Sprouts game with reduced canonical trees, 2009
- Black and White Sprouts (Memento vom 6. März 2010 auf WebCite) auf World Game Of Sprout Association (im WebCite-Archiv)