Scree-Test
Der Scree-Test, auch Ellenbogenkriterium genannt, ist ein graphisches Verfahren zur Bestimmung der optimalen Faktorenzahl bei der Faktorenanalyse. Das Kriterium wurde in den 1960er Jahren von dem US-amerikanischen Psychologen Raymond Bernard Cattell entwickelt und findet aufgrund seiner Einfachheit bis heute Verwendung.
Hintergrund zur Faktorenauswahl
Bei der Faktorenanalyse sollen nur diejenigen Faktoren extrahiert werden, die einen bedeutenden Teil der Varianz erklären und daher einen hohen Eigenwert besitzen. Dies ist bei dem ersten Faktor der Fall, in der Regel auch bei einigen weiteren Faktoren, wenngleich die Eigenwerte in der Regel stark abnehmen. Ab einem gewissen Faktor verharrt dann die zusätzliche Varianz, die durch jeden zusätzlichen Faktor erklärt wird, auf niedrigem Niveau.
Die Auswahl der Faktoren dient in erster Linie der Gewinnung von aussagekräftigen, gut interpretierbaren Ergebnissen und ist damit nur eingeschränkt objektivierbar.
Grundannahme
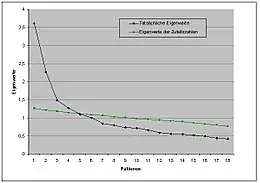
Die Grundannahme ist, dass nur diejenigen Faktoren bedeutsam seien, die eine stärkere Korrelation repräsentieren als die Korrelation von Zufallszahlen. Der Scree-Test macht sich nun die Tatsache zunutze, dass – im Gegensatz zu den Eigenwerten korrelierter Daten – die Eigenwerte von Zufallszahlen typischerweise annähernd konstant verlaufen.
Vorgehensweise
Zur Anwendung des Scree-Tests werden die abfallend sortierten Eigenwerte der möglichen Faktoren in einem sogenannten Eigenwertediagramm oder auch Scree-Plot betrachtet. Der Plot ist so benannt, da er einer Schuttrampe (englisch scree) ähnelt.

Nachdem die der Größe nach geordneten Eigenwerte der korrelierten Daten zunächst steil abfallen, zeichnet sich typischerweise eine Knickstelle („Ellenbogen“) ab. Die rechts daneben liegenden Werte stagnieren annähernd auf niedrigem Niveau; sie gelten als nicht bedeutsam, da sie sich in etwa auf (oder sogar unter) dem Niveau von Zufallskorrelationen bewegen.
Die links neben der Knickstelle liegenden Eigenwerte hingegen gelten als bedeutsam und sind in der Faktorenanalyse zu extrahieren. Bei mehreren Knickstellen ist der stärkere bzw. weiter rechts stehende Knick zu berücksichtigen. Gibt es keine Knickstelle, so hilft das Ellenbogenkriterium nicht weiter.
Kritik und Weiterentwicklungen
Kritik an der Objektivität
Der erstmals in Cattell (1966) publizierte Scree-Test wird häufig aufgrund seiner geringen Objektivität kritisiert. Ist keine eindeutige Knickstelle auszumachen, besteht Raum zur Interpretation.
Parallelanalyse
Die von J. L. Horn (1965) vorgestellte – oft als Parallelanalyse bezeichnete – Modifikation legt über das Eigenwertediagramm der korrelierten Daten ein zweites Eigenwertediagramm. Nur diejenigen untersuchten Eigenwerte, die höher sind als die Zufallseigenwerte, gelten als bedeutsam. Trotz der starken Ähnlichkeit kommen die beiden Varianten häufig zu abweichenden Ergebnissen. Obwohl Horns Modifikation objektiv anwendbar ist, konnte er Cattells Scree-Test nie verdrängen.
Die zweiten Eigenwerte werden berechnet unter der Annahme, dass
- die Variablen unkorreliert sind, d. h. die Korrelations- oder Kovarianzmatrix ist eine Diagonalmatrix und
- die Daten multivariat normalverteilt sind.
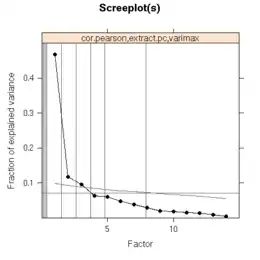
Auf dieser Basis werden B Zufallsdatensätze mit der gleichen Anzahl von Variablen und Beobachtungen wie der betrachtete Datensatz erzeugt und die Eigenwerte der dazugehörigen empirischen Korrelations- bzw. Kovarianzmatrix berechnet. Die B größten Eigenwerte approximieren die Verteilung des größten Eigenwertes, die B zweitgrößten Eigenwerte approximieren die Verteilung des zweitgrößten Eigenwertes, ... Dann wird z. B. das 95 % Quantil der B größten Eigenwerte als Grenze für den größten Eigenwert genommen. Ist der größte Eigenwert der Daten größer als , so ist dieser Eigenwert bedeutsam. Die zweite Abbildung rechts zeigt für den Boston Housing Datensatz mit der fallenden grauen Linie das Horn Kriterium.
Standard Error Scree
Neben weiteren, in den Folgejahrzehnten entstandenen Weiterentwicklungen und Verbesserungen stellen Zoski und Jurs (1996) einen Standard Error Scree vor.
Kritik an der Grundannahme
Auch die Grundannahme, dass Eigenwerte unterhalb von Zufallseigenwerten bedeutungslos seien, wurde von manchen Wissenschaftlern bezweifelt. Sie allein aufgrund ihrer Größe mit Zufalls- oder Fehlerergebnissen gleichzusetzen, sei unzulässig.
Alternativen
Als Alternative kommt das rigidere Kaiser-Guttman-Kriterium in Frage, das jedoch bisweilen zu schlecht interpretierbaren Lösungen führt.
Grundsätzlich sollten mehrere Kriterien herangezogen werden. Insbesondere im Zweifelsfall bietet es sich an, mehrere Faktorenzahlen durchzurechnen und im Hinblick auf Ladungen und Interpretierbarkeit zu überprüfen.
Literatur
Primärliteratur
- Cattell, R. B. (1966). The scree test for the number of factors. Multivariate Behavioral Research 1, 245–276, doi:10.1207/s15327906mbr0102_10.
- Horn, J. L. (1965). A rationale and test for the number of factors in factor analysis. Psychometrika, 30, 179–185, doi:10.1007/BF02289447.
- Zoski, Keith W., Jurs Steven G. (1996): An objective counterpart to the visual scree test for factor analysis: The standard error scree. Educational and Psychological Measurement, 56, 443–451, doi:10.1177/0013164496056003006.
Sekundärliteratur
- Bortz, J. & Schuster, C. (2010). Faktorenanalyse. In: Statistik für Human- und Sozialwissenschaftler. 7. Auflage (S. 385–433). Berlin und Heidelberg: Springer, ISBN 978-3-642-12769-4, doi:10.1007/978-3-642-12770-0_23.