Schellbachstreifen

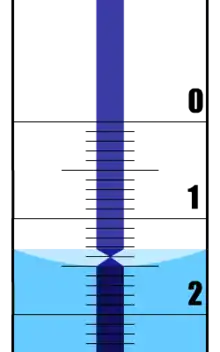
Ein Schellbachstreifen ist ein breiter weißer Milchglasstreifen auf der Rückseite einer Bürette, auf dem sich ein 1 mm schmaler, farbiger (meist blauer) Längsstreifen befindet, der den Flüssigkeitsstand in der Bürette durch zwei sich treffende Pfeilspitzen visuell anzeigt. Die wird verursacht durch den Meniskus der Flüssigkeitsoberfläche in der Bürette. Dadurch wird die Ablesegenauigkeit verbessert.[1][2]

Dieser Artikel wurde auf der Qualitätssicherungsseite der Redaktion Chemie eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Chemie formal und inhaltlich auf ein in der Wikipedia gewünschtes Niveau zu bringen. Wir sind dankbar für deine Mithilfe, bitte beteilige dich an der Diskussion (neuer Eintrag) oder überarbeite den Artikel entsprechend.

Schema einer Bürette mit Schellbachstreifen

Die Benennung geht zurück auf den deutschen Mathematiker und Physiker Karl Heinrich Schellbach (1805–1892).

Besteht die Bürette aus einem kreiszylindrischen Glasrohr, so erscheint der unterhalb des Flüssigkeitsmeniskus befindliche Teil des Schellbachstreifens gegenüber dem über dem Meniskus – anders als in der Abbildung gezeigt – verbreitert. Dies liegt an der Vergrößerungswirkung des gefüllten Zylinders. Im Falle von Wasser oder wässrigen Lösungen ist der Vergrößerungsfaktor ziemlich genau zwei. Dies lässt sich mit Hilfe der Abbildungsgleichungen bei Lichtbrechung an einer einzelnen zylindrischen Fläche quantitativ erfassen. Nimmt man die Rohrwand als dünn an, so berechnet man die laterale Vergrößerung des gefüllten Zylinderrohrs zu

$V={\frac {1}{1-{\frac {n-1}{nR}}g}}$

Hierbei ist $R$ der Radius des Rohres und $g$ bezeichnet den Abstand des Objekts im Rohr von der Vorderwand. $n$ ist der Brechungsindex der Flüssigkeit. Für Wasser im Sichtbaren ist $n=1.33$ . Da sich der Schellbachstreifen an der Rückwand des Zylinderrohrs befindet, gilt $g=2R$ , so dass $V=1/0.504\approx 2$ .

Einzelnachweise

Siegfried Ebel und Hermann J. Roth (Herausgeber): Lexikon der Pharmazie, Georg Thieme Verlag, 1987, S. 583–584, ISBN 3-13-672201-9.
Otto-Albrecht Neumüller (Hrsg.): Römpps Chemie-Lexikon. Band 5: Pl–S. 8. neubearbeitete und erweiterte Auflage. Franckh'sche Verlagshandlung, Stuttgart 1987, ISBN 3-440-04515-3, S. 3707.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Ebel-1] Siegfried Ebel und Hermann J. Roth (Herausgeber): Lexikon der Pharmazie, Georg Thieme Verlag, 1987, S. 583–584, ISBN 3-13-672201-9.

[Römpp-2] Otto-Albrecht Neumüller (Hrsg.): Römpps Chemie-Lexikon. Band 5: Pl–S. 8. neubearbeitete und erweiterte Auflage. Franckh'sche Verlagshandlung, Stuttgart 1987, ISBN 3-440-04515-3, S. 3707.