Satz von Steiner-Lehmus
Der Satz von Steiner-Lehmus ist ein Satz der Elementargeometrie über Dreiecke.
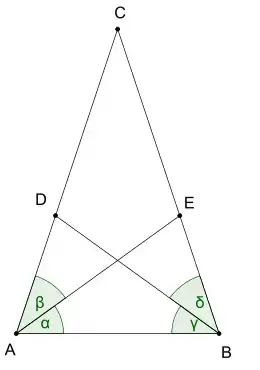
Er wurde zuerst von Christian Ludolf Lehmus formuliert und dann von Jakob Steiner bewiesen.
- Sind in einem Dreieck zwei Winkelhalbierende gleich lang, so ist es gleichschenklig.
Der Satz wurde zum ersten Mal 1840 in einem Brief von C. L. Lehmus an Charles-François Sturm erwähnt, in welchem dieser Sturm um einen elementargeometrischen Beweis der Aussage bat. Sturm verbreitete das Problem unter anderen Mathematikern und Jakob Steiner war einer der Ersten, der einen Beweis erbrachte. Seitdem wurde der Satz zu einem beliebten Gegenstand der Elementargeometrie, zu dem in den folgenden 160 Jahren zahlreiche Publikationen erschienen.[1][2]
Literatur
- John Horton Conway, Alex Ryba: The Steiner-Lehmus Angle Bisector Theorem. In: Mircea Pitici (Hrsg.): The Best Writing on Mathematics 2015. Princeton University Press, 2016, ISBN 978-1-4008-7337-1, S. 154–166
- Alexander Ostermann, Gerhard Wanner: Geometry by Its History. Springer, 2012, S. 224–225
- S. Abu-Saymeh, M. Hajja, H. A. ShahAli: Another Variation on the Steiner-Lehmus Theme. In: Forum Geometricorum, 8, 2008, S. 131–140
- David Beran: SSA and the Steiner-Lehmus Theorem. In: The Mathematics Teacher, Vol. 85, No. 5 (Mai 1992), S. 381–383 (JSTOR 27967647)
- C. F. Parry: A Variation on the Steiner-Lehmus Theme. In: The Mathematical Gazette, Vol. 62, No. 420 (Juni 1978), S. 89–94 (JSTOR 3617662)
- Mordechai Lewin: On the Steiner-Lehmus Theorem. In: Mathematics Magazine, Vol. 47, No. 2 (März 1974), S. 87–89 (JSTOR 2688873)
- V. Pambuccian, H. Struve, R. Struve: The Steiner-Lehmus theorem and triangles with congruent medians are isosceles hold in weak geometries. In: Beiträge zur Algebra und Geometrie, Band 57, 2016, Nr. 2, S. 483–497
- V. Pambuccian, Negation-free and contradiction-free proof of the Steiner-Lehmus theorem. In Notre Dame Journal of Formal Logic, Vol. 59 (2018), S. 75–90
Weblinks
- Florian Modler: Vergessene Sätze am Dreieck (Teil 2). In: Matroids Matheplanet, 27. August 2006
- Eric W. Weisstein: Steiner-Lehmus theorem. In: MathWorld (englisch).
- Paul Yiu: Euclidean Geometry Notes (PDF; 1,0 MB) Skript, Florida Atlantic University, S. 15–16 (englisch)
- Torsten Sillke: Steiner-Lehmus Theorem. Sammlung verschiedener Beweise zum Satz von Steiner-Lehmus (englisch)
Einzelnachweise
- Harold Scott MacDonald Coxeter, Samuel L. Greitzer: Geometry Revisited. Random House, New York 1967, S. 14–16 (The Steiner–Lehmus Theorem)
- Diane und Roy Dowling: The Lasting Legacy of Ludolph Lehmus (PDF; 388 kB). In: Manitoba Math Links 2, 3, 2002, S. 3–4.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.