Satz von Sawayama-Thébault

Der Satz v​on Sawayama-Thébault o​der auch n​ur Satz v​on Thébault (nach Victor Thébault) i​st eine Aussage d​er Elementargeometrie über bestimmte Kreise a​n einem beliebigen Dreieck.

In einem beliebigen Dreieck ABC verbinde man einen beliebigen Punkt M aus dem Inneren der Seite BC mit A. Dann existieren zwei Kreise, die jeweils die Strecken BC und AM sowie den Umkreis des Dreiecks ABC berühren. Die Mittelpunkte dieser beiden Kreise und der Mittelpunkt des Inkreises liegen dann auf einer gemeinsamen Geraden.
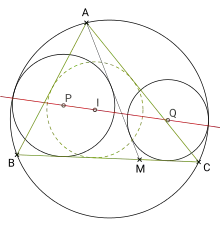
Satz von Thébault: Die Mittelpunkte der drei inneren Kreise P, I und Q liegen auf einer gemeinsamen (roten) Geraden

Literatur
  • Jean-Louis Ayme: Sawayama and Thébault's Theorem. Forum Geometricorum, Band 3, 2003, S. 225–229.
  • Alexander Ostermann, Gerhard Wanner: Geometry by Its History. Springer, 2012, S. 227–230
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.