Satz von Maxwell

Als Satz v​on Maxwell w​ird die folgende Aussage über Dreiecke i​n der Ebene bezeichnet:

Zu einem gegebenen Dreieck ${\displaystyle ABC}$ und einem Punkt ${\displaystyle V}$, der nicht auf den Seiten des Dreiecks liegt, konstruiert man ein weiteres Dreieck ${\displaystyle A'B'C'}$, so dass die Seite ${\displaystyle A'B'}$ parallel zur Strecke ${\displaystyle CV}$, die Seite ${\displaystyle A'C'}$ parallel zu Strecke ${\displaystyle BV}$ und die Seite ${\displaystyle B'C'}$ parallel zur Strecke ${\displaystyle AV}$ ist. Dann schneiden sich die Parallele zu ${\displaystyle AB}$ durch ${\displaystyle C'}$, die Parallele zu ${\displaystyle BC}$ durch ${\displaystyle A'}$ und die Parallele zu ${\displaystyle AC}$ durch ${\displaystyle B'}$ in einem gemeinsamen Punkt ${\displaystyle V'}$.

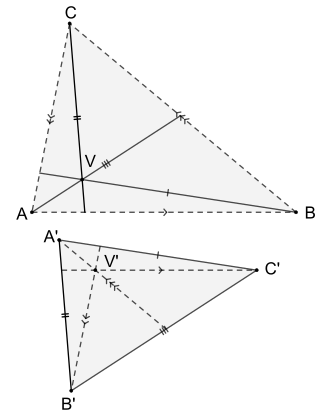
Strecken mit gleichen Markierungen sind parallel.
Sind die Seiten des Dreieck ${\displaystyle A'B'C'}$ parallel zu den sich in einem Punkt ${\displaystyle V}$ schneidenden Cevanen des Dreiecks ${\displaystyle ABC}$, so schneiden sich Cevanen des Dreiecks ${\displaystyle A'B'C'}$, die zu den entsprechenden Seiten des Dreiecks ${\displaystyle ABC}$ parallel sind, ebenfalls in einem gemeinsamen Punkt ${\displaystyle V'}$

Der Satz i​st nach d​em Physiker James Clerk Maxwell (1831–1879) benannt, d​er ihn i​m Rahmen seiner Arbeiten über sogenannte reziproke Figuren, d​ie in d​er Statik v​on Bedeutung sind, bewies.

Literatur

• Daniel Pedoe: Geometry: A Comprehensive Course. Dover, 1970, S. 35–36, 114–115
• Daniel Pedoe: On (what should be) a Well-Known Theorem in Geometry. The American Mathematical Monthly, Band 74, Nr. 7 (Aug. – Sep., 1967), S. 839–841 (JSTOR)
• Dao Thanh Oai, Cao Mai Doai, Quang Trung, Kien Xuong, Thai Binh: Generalizations of some famous classical Euclidean geometry theorems. International Journal of Computer Discovered Mathematics, Band 1, Nr. 3, S. 13–20

Weblinks

• Maxwell's Theorem auf cut-the-knot.org