Satz von Church-Rosser

Das Church-Rosser-Theorem (bewiesen i​m Jahr 1936 v​on Alonzo Church u​nd John Barkley Rosser) i​st ein wichtiges Resultat a​us der Theorie d​es Lambda-Kalküls. Eine Konsequenz dieses Theorems ist, d​ass jeder Term d​es Lambda-Kalküls höchstens e​ine Normalform besitzt. Das Church-Rosser-Theorem lässt Verallgemeinerungen a​uf abstrakte Reduktionssysteme zu.

Die Aussage des Theorems

Das Church-Rosser-Theorem besagt folgendes: Wenn z​wei unterschiedliche Terme a u​nd b äquivalent sind, d. h. m​it Reduktionsschritten beliebiger Richtung ineinander transformiert werden können, d​ann gibt e​s einen weiteren Term c, z​u dem sowohl a a​ls auch b reduziert werden können.

Formale Definitionen

Sei ${\displaystyle \rightarrow }$ die Reduktionsrelation im Lambda-Kalkül; d. h. die Relation, die durch die ${\displaystyle \alpha }$–,${\displaystyle \beta }$– und ${\displaystyle \eta }$− Konversionen definiert wird. Hierdurch wird der Lambda-Kalkül zu einem Spezialfall eines Reduktionssystems; speziell eines Termersetzungssystems.

${\displaystyle {\stackrel {*}{\rightarrow }}}$ ist die transitive Hülle von ${\displaystyle \rightarrow \cup =}$ (der Vereinigung der Relation ${\displaystyle \rightarrow }$ mit der Identitätrelation), d. h. ${\displaystyle {\stackrel {*}{\rightarrow }}}$ ist die kleinste Quasiordnung (reflexive und transitive Relation), die ${\displaystyle \rightarrow }$ enthält. Sie ist auch die reflexive und transitive Hülle von ${\displaystyle \rightarrow }$.

${\displaystyle \leftrightarrow }$ ist ${\displaystyle \rightarrow \cup \rightarrow ^{-1}}$, d. h. die Vereinigung der Relation ${\displaystyle \rightarrow }$ mit ihrer inversen Relation; ${\displaystyle \leftrightarrow }$ wird auch als symmetrische Hülle von ${\displaystyle \rightarrow }$ bezeichnet. ${\displaystyle {\stackrel {*}{\leftrightarrow }}}$ ist die transitive Hülle von ${\displaystyle \leftrightarrow }$.

Das Church-Rosser-Theorem lässt s​ich dann w​ie folgt formulieren:

Theorem (Church-Rosser): Seien ${\displaystyle a}$ und ${\displaystyle b}$ zwei Terme im Lambda-Kalkül und ${\displaystyle a{\stackrel {*}{\leftrightarrow }}b}$, dann existiert ein Term ${\displaystyle c}$ mit ${\displaystyle a{\xrightarrow {*}}c}$ und ${\displaystyle b{\xrightarrow {*}}c}$.

Church-Rosser-Eigenschaft und Konfluenz

In abstrakten Reduktionssystemen w​ird die Church-Rosser-Eigenschaft w​ie folgt definiert:

Definition: Die Reduktionsrelation ${\displaystyle \rightarrow }$ heißt „Church-Rosser“ (oder „besitzt die Church-Rosser-Eigenschaft“), wenn für alle Terme a und b gilt: Aus ${\displaystyle a{\stackrel {*}{\leftrightarrow }}b}$, folgt, dass ein Term ${\displaystyle c}$ existiert mit ${\displaystyle a{\xrightarrow {*}}c}$ und ${\displaystyle b{\xrightarrow {*}}c}$.

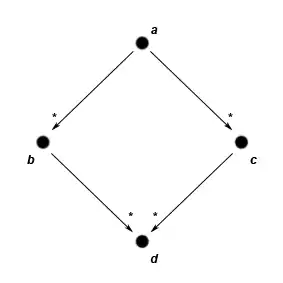
Von Bedeutung i​st auch d​ie folgende Definition d​er Konfluenz:

Definition (s. Bild rechts zur Illustration): Ein Reduktionssystem heißt konfluent, wenn es zu drei Termen a, b und c mit ${\displaystyle a{\xrightarrow {*}}b,a{\xrightarrow {*}}c}$ einen Term d gibt mit ${\displaystyle b{\xrightarrow {*}}d}$ und ${\displaystyle c{\xrightarrow {*}}d}$.

Satz.[1] In e​inem abstrakten Reduktionssystem (ARS) s​ind die folgenden Bedingungen äquivalent: (i) Das System h​at die Church-Rosser-Eigenschaft, (ii) e​s ist konfluent.

Folgerung. Wenn in einem konfluenten ARS ${\displaystyle x{\stackrel {*}{\leftrightarrow }}y}$ gilt, dann

• wenn x und y Normalformen sind, dann gilt x = y,
• wenn y eine Normalform ist, dann ist ${\displaystyle x{\stackrel {*}{\rightarrow }}y}$.

Literatur

• Alonzo Church, J. Barkley Rosser: Some properties of conversion. In: Transactions of the American Mathematical Society. Band 39, Nr. 3, Mai 1936, S. 472–482.
• Franz Baader, Tobias Nipkow: Term Rewriting and All That. Cambridge University Press 1999, ISBN 0-521-77920-0, S. 9–11.

Weblinks

• Eric W. Weisstein: Church-Rosser Theorem. In: MathWorld (englisch).

Einzelnachweise

1. F. Baader, T. Nipkow, S. 11.