Randkanalmodell
Mit dem Randkanalmodell lässt sich das Zustandekommen des Quanten-Hall-Effekts und des Schubnikow-de-Haas-Effekts in zweidimensionalen Elektronengasen erklären. Durch das Berücksichtigen von Randeffekten bilden sich Randkanäle, die die Anomalitäten der obigen Effekte erklären können.
Quantenmechanische Deutung
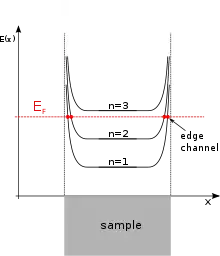
Bei Anlegen eines externen Magnetfeldes ändert sich die Zustandsdichte der Elektronen. Es bilden sich dadurch Landauniveaus aus. Dies sind diskrete, bei kleinen Feldern spinentartete Energieniveaus. Die Beschreibung durch das Randkanalmodell nimmt an, dass sich das Ferminiveau zwischen zwei Landauniveaus befindet und das System im Grundzustand ist. Alle Niveaus unterhalb des Ferminiveaus sind folglich vollbesetzt.
An den Rändern einer Probe muss das sonst vernachlässigbare Randpotential in die Schrödingergleichung mit einbezogen werden. Dies führt dazu, dass die Landauniveaus nach oben gebogen werden (dieses Ansteigen kann man sich plausibel machen, wenn man die Austrittsarbeit als Analogon heranzieht – um die Hürde "Rand" überwinden zu können, muss Energie zugeführt werden). Durch dieses Ansteigen der Niveaus ergeben sich Schnittpunkte der Energieniveaus mit der Fermi-Energie. Es entstehen Zustände an der Fermikante, die als Randkanäle bezeichnet werden. Dadurch wird es den Ladungsträgern ermöglicht, sich frei zu bewegen.
Klassische Deutung

Klassisch kann man die Randkanäle durch sogenannte "skipping orbits" ("hüpfende Umlaufbahnen") beschreiben. Elektronen werden durch ein Magnetfeld wegen der Lenzschen Regel auf eine gekrümmte Bahn gezwungen, die Zyklotronbahn. Befindet sich ein Elektron im Inneren der Probe, so kann die Kreisbahn ohne weitere Einschränkung (Streuung wird nicht betrachtet) durchlaufen werden. Dies entspricht der idealen Betrachtung ohne Randeffekte.
Betrachtet man Elektronen mit einem Abstand kleiner als der Zyklotronradius zum Rand der Probe, so wird aus geometrischen Überlegungen klar, dass diese keine ungestörten Kreisbahnen mehr durchlaufen können. Sie stoßen innerhalb eines Umlaufs an den Rand und werden dort reflektiert. Von dieser Bewegung leitet sich die Bezeichnung "skipping orbits" ab. Dadurch ergibt sich eine Nettobewegung der Ladungsträger entlang der Begrenzung, welche Stromfluss ermöglicht. Der Stromfluss ist deshalb auf die Ränder der Probe eingeschränkt.
Es ergibt sich eine sehr effektive räumliche Trennung von Ladungsträgern, die sich in verschiedene Richtungen bewegen. Die elektronische Wellenfunktion fällt schnell ab, sodass die Überlappung der Zustände verschiedener Ränder sehr klein wird. Weiterhin können sie nicht auf die andere Seite der Probe streuen, da es durch die Lage der Fermi-Energie zwischen zwei Landauniveaus keine freien Zustände gibt, in die gestreut werden könnte. Die Streuwahrscheinlichkeit zwischen Ladungsträgern ist somit effektiv unterdrückt. Dadurch geht auch die Wahrscheinlichkeit für Rückstreuung gegen 0 und die Leitung wird somit widerstandsfrei. Dieser Effekt wird nach ihren Entdeckern Schubnikow-de-Haas-Effekt genannt.
Dies bedeutet, dass Elektronen, die an einer Stelle (z. B. einem Kontakt) in einen Randkanal eintreten, sich bis zum nächsten Kontakt fortbewegen müssen. Auch nach Streuung werden sie weiter in diese Richtung gezwungen. Die zu Recht aufgeworfene Frage, wie das Ferminiveau zwischen einem besetzten und unbesetzten Landauniveau sein kann, wird durch Störstellen und Fremdatome erklärt. Ohne sie könnte das Ferminiveau nicht dazwischen liegen. Dies wird auch experimentell so bestätigt. Bei äußerst reinen Proben werden die gemessenen Oszillationen wieder schwächer; bei zu großer Störstellendichte wird der Effekt durch hohe Streuwahrscheinlichkeit unterdrückt. In diesem Fall können die Ladungsträger keine komplette Zyklotronbahn mehr durchlaufen und mit sich selbst interferieren.
Literatur
- S. Datta: Electronic transport in mesoscopic systems. Cambridge University Press, Cambridge 1995, ISBN 978-0-521-59943-6 (englisch).
- J. H. Davies: The physics of low-dimensional semiconductors: An introduction. Cambridge University Press, Cambridge 1998, ISBN 978-0-521-48491-6 (englisch).
- D. Yoshioka: The Quantum Hall Effect. Springer Verlag, Berlin 2002, ISBN 978-3-540-43115-2 (englisch).
- G. Czycholl: Theoretische Festkörperphysik. Springer Verlag, Berlin 2004, ISBN 3-540-20824-0.
Weblinks
- D. Tong: Lectures on the Quantum Hall Effect. 2016, S. 46ff, arxiv:1606.06687 (englisch).
- Jürgen Smoliner: Vorlesungsskripten zur VO Halbleiterelektronik am Institut für Festkörperelektronik, TU Wien. 2017, S. 357ff (tuwien.ac.at [PDF]).
- Fortgeschrittenen-Praktikum: Der Quanten-Hall-Effekt. Uni Giessen, I. Physikalisches Institut, Abt. für Mikro- und Nanostrukturierung, Prof. Dr. Peter J. Klar.