Rainbow Table
Die Rainbow Table (engl. für Regenbogentabelle) ist eine von Philippe Oechslin entwickelte Datenstruktur, die eine schnelle, speichereffiziente Suche nach der ursprünglichen Zeichenfolge (in der Regel ein Passwort) für einen gegebenen Hashwert ermöglicht. Die Suche über eine Rainbow Table ist erheblich schneller als bei der Brute-Force-Methode, allerdings ist der Speicherbedarf höher. Solch ein Kompromiss wird Time-Memory Tradeoff genannt.
Vorausgesetzt wird eine Hashfunktion ohne Salt, wie es z. B. bei den Passwörtern für frühere Windows-Versionen und bei vielen Routern der Fall ist. Vergleichsweise umfangreiche Tabellen wurden für LM Hashes und MD5 berechnet und stehen aus diversen Quellen zur Verfügung.
Verwendung finden Rainbow Tables bei der Wiederherstellung von Passwörtern, innerhalb der IT-Forensik, bei Penetrationstests und beim Passwortcracken.
Überblick
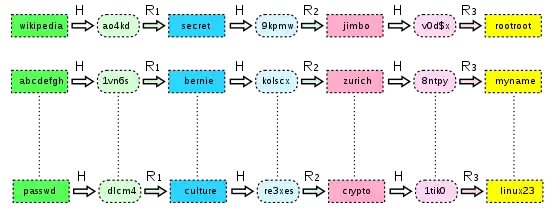
Eine Rainbow Table ist eine kompakte Repräsentation von zusammenhängenden Passwortsequenzen, sogenannten Ketten (chains). Jede dieser Ketten startet mit einem initialen Kennwort, welches durch eine Hashfunktion geleitet wird. Der resultierende Hash wird wiederum durch eine Reduktionsfunktion geleitet mit dem Ergebnis, ein weiteres potentielles Klartextkennwort zu haben. Dieser Prozess wird für eine vorgegebene Anzahl wiederholt, und schließlich das erste Kennwort der Kette zusammen mit dem Kennwort aus dem letzten Hashwert gespeichert.
Beim Erstellen der Tabelle ist darauf zu achten, dass einerseits kein Kennwort, welches in einer Kette vorkommt, als Startkennwort verwendet wird (Kollision), dass aber andererseits alle möglichen Kennwörter in der Tabelle vorkommen. Die Tabellen werden nur einmalig erstellt und dienen dann als Nachschlagetabelle.
Um ein Kennwort herauszufinden, wird ein zweistufiger Prozess benötigt. Zunächst wird der Hash des gesuchten Kennworts durch die oben beschriebene Hash-Reduktion-Sequenz geführt, bis das Ergebnis der Reduktion in der Tabelle der letzten Kettenglieder vorkommt (die „rechte Seite“ der Tabelle). Damit erhält man das Startkennwort der Kette und kann im zweiten Schritt von diesem ausgehend die Hash-Reduktion-Sequenz anwenden, um das gesuchte Kennwort zu erhalten.
Die Länge der Kette, also die Anzahl der Iterationen zur Erstellung der Tabellen, wirken sich auf die Größe der Tabelle aus: Je länger die Iterationen gewählt werden, desto kleiner ist die entstehende Tabelle. Im einfachsten Fall ist die Anzahl der Iterationen gleich 1, sodass die Tabelle alle Kennwort-Hash-Paare enthält.
Funktionsweise
Eine Hashfunktion ordnet einer Binärfolge beliebiger Länge eine Binärfolge fester Länge zu. Bei der Hashfunktion MD5 beträgt diese Ausgabelänge 128 Bit oder 32 4-Bit-Zeichen. Zu einer zufälligen Zeichenkette mit der Länge wird ein Hashwert berechnet. Dieses Ergebnis der Hashfunktion (mit Länge 32) wird durch eine Reduktionsfunktion R in eine neue Zeichenkette umgewandelt, die wieder Länge besitzt. Weil die Hintereinanderausführung von Hashfunktion und Reduktionsfunktion die Länge der Zeichenkette nicht ändert, können diese beiden Schritte beliebig oft abwechselnd wiederholt werden. Die Folge der Zwischenergebnisse bildet am Ende eine Kette (Chain). Gespeichert werden Anfangs- und Endwert dieser Kette. Diese Schrittfolge wird ebenfalls -mal wiederholt und bildet eine universelle Rainbow Table.
Reduktionsfunktion
Die Reduktionsfunktion verkürzt einen Hashwert auf Zeichen. Jede dieser Reduktionen liefert z. B. durch MD5 eine neue „eindeutige“ 128 bit Zeichenkette, oder eine Kollision. Als eine Kollision bezeichnet man dabei einen Hashwert, der durch verschiedene Ausgangszeichenfolgen erzeugt werden kann. Um Kollisionen zu vermeiden, verwendet man verschiedene Reduktionsfunktionen, die periodisch angewendet eine eindeutige Zuordnung der Eingangs-Zeichenkette und des Ausgangshashes ermöglichen. Dieses Verfahren stellt eine effizientere Methode für n-stellige Zeichenketten dar als beispielsweise ein Brute-Force-Angriff mit Schlüsselsuche von [a-//////], da bei letzterem viele Zeichenketten in Hashes umgewandelt werden, die mit hoher Wahrscheinlichkeit niemals fallen bzw. gewählt werden.
Bei schlecht programmierten oder trivialen Reduktionsfunktionen treten nach wenigen Läufen Kollisionen auf, die zu Wiederholungen der reduzierten Texte und somit auch der Hashes führen. Solche internen Schleifen führen dann dazu, dass der Algorithmus versagt: Man berechnet mühsam Tausende von Elementen, und nur einige wenige davon sind eindeutig unterscheidbar.
Anwendung
Gesucht wird in diesem Beispiel die Zeichenfolge, deren MD5-Hashwert in der Hexadezimaldarstellung 97fae39bfd56c35b6c860aa468c258e0 entspricht (Domino). Der herkömmliche Weg, alle MD5-Hashes für alle möglichen Variationen zu berechnen und diese zu vergleichen, ist sehr rechenintensiv und muss bei neuen Suchläufen wiederholt werden.
Sinnvoll wäre es nun, alle bereits berechneten Hashes in einer Datenbank zu speichern und bei erneuten Suchläufen nur noch vergleichen zu müssen, ob der gesuchte Hash schon bekannt ist. Bei einer Suche über 64 mögliche Zeichen [A-Za-z0-9./], die jede Stelle des Eingangstextes haben könnte, ergeben sich bei 6 Stellen Variationen. Werden nun Text und Hash in einer Datenbank gespeichert, so werden pro Paar 16 Byte für den Hash und 6 Byte für den Plaintext benötigt und somit für die kompletten Daten etwa 1,4 Terabyte.
Diese Datenmengen lassen sich meistens nicht verarbeiten und müssen reduziert werden.
Sinnvoller Mittelweg: Rainbow Table
Anstatt alle Werte samt Schlüsseln zu speichern, werden nur die anfängliche Zeichenkette und die letzte Zeichenkette einer -elementigen Kette gespeichert. Auf diese Weise lassen sich Hashes durch einen Start- und Endwert repräsentieren und in vergleichsweise kurzer Zeit neu berechnen und damit der Eingabetext wiederfinden. Bildet sich aus einem reduzierten Hash (= Plaintext) ein Endwert, so wird diese Kette vom Startwert aus neu berechnet, bis sich der gegebene Hash ergibt; der diesem vorausgehende Text ist der gesuchte Ursprungstext. Bei einer Ketten-Länge von werden also nur 9.999 Hash-Berechnungen gebraucht, um den Ursprungstext zu einem Hash zu finden.
Die Wahrscheinlichkeit, aus den reduzierten Hashes genau den gesuchten Eingangstext zu erhalten, ist abhängig von der Güte der Reduktionsfunktion(en) und den Parametern bei der Erstellung der Rainbow Table, da nur die reduzierten Hashes (= Plaintexts) später gefunden werden können. Wenn die Reduktionsfunktion(en) beispielsweise nur auf Zahlen reduzieren, kann der Plaintext „Domino“ nicht gefunden werden. Wenn die Reduktionsfunktion(en) auf sieben Stellen reduzieren (von 32), dann werden 6-stellige Plaintexts nicht berechnet und auch hier kann „Domino“ nicht gefunden werden.
Perfekte und nicht perfekte Rainbow Tables
In einer perfekten Rainbow Table befinden sich in den Ketten keine Passwörter die doppelt vorkommen. Somit hat eine perfekte Rainbow Table die geringste Anzahl von Ketten, um alle Passwörter darstellen zu können. Jedoch steigt der Berechnungsaufwand an, um die perfekte Rainbow Table zu erzeugen. In nicht perfekten Rainbow Tables kommen redundante Passwörter in den Ketten vor. Sie sind schneller zu erzeugen, nehmen jedoch mehr Speicherplatz ein als eine perfekte Rainbow Table.
Gegenmaßnahmen
Passwörter werden vor dem Speichern mit einer kryptographischen Hashfunktion gehasht, damit aus der Liste der gespeicherten Hashwerte nicht auf das Passwort geschlossen werden kann, falls die Datei mit den Passwörtern gestohlen wird. Rainbow Tables machen aber genau das möglich. Um die Passwörter zu schützen, gibt es verschiedene Gegenmaßnahmen, die den Einsatz von Rainbow Tables weniger effizient machen sollen.
Kennwortlänge
Die Größe einer Rainbow Table steigt mit der Länge der Kennwörter, für die sie generiert werden soll. Je nach Hashtyp ist ab einer gewissen Kennwortlänge die Berechnung einer Rainbow Table nicht mehr wirtschaftlich, sowohl was die Dauer der Generierung (Stromkosten) als auch den Platzbedarf der Tabellen angeht. Lange Kennwörter entstehen z. B. bei der Verwendung von Sätzen statt eines Wortes (siehe Passphrase).
Salts
Eine weitere Methode, die Generierung von Rainbow Tables unwirtschaftlich zu machen, ist der Einsatz von Salt. Dabei wird an das Passwort vor dem Hashen ein – im Idealfall – zufällig generierter Wert, das Salt, angehängt. Das Salt wird zusammen mit dem Hashwert gespeichert, um das Passwort später überprüfen zu können, es ist also kein Geheimnis.
Beispiel
- Passwort, genau 6 Stellen, nur Zahlen erlaubt: 123456
- Salt, beliebige Kombination dreier Großbuchstaben: ABC
Geshasht wird nun also nicht 123456, sondern 123456ABC. Eine Rainbow Table genau für dieses Salt zu erzeugen ist nicht wesentlich aufwändiger als ohne Salt, da der hintere Teil des Passwortes (das Salt) ja bereits bekannt ist. Die Tabelle müsste also für alle möglichen Kombinationen mit ABC am Ende erzeugt werden, was natürlich genauso viele Einträge sind wie ohne Salt am Ende:
| Passwort | Hash |
|---|---|
| 111111ABC | hash(111111ABC) |
| 111112ABC | hash(111112ABC) |
| ... | ... |
| 999999ABC | hash(999999ABC) |
Der eigentliche Clou liegt nun darin, dass das Salt nicht immer gleich bleibt, sondern bei jedem Passwort zufällig generiert wird. Eine Rainbow Table für das Salt ABC nützt uns bei einem Salt von XYZ daher nichts. Für eben diesen müsste nun erneut eine Rainbow Table erzeugt werden. Damit würde sich der Aufwand um die Zahl der möglichen Salts vervielfachen, weil für jedes mögliche Salt eine Rainbow Table erstellt werden müsste.
Da nicht mehr eine Rainbow Table verwendet werden kann, um alle Passwörter zu finden, wird diese Methode unwirtschaftlich bzw. technisch nicht realisierbar. Salts können aber kurze Passwörter nicht schützen – sie erhöhen nur den Aufwand beim Brute-Forcen, wenn mehrere vorliegen, verhindern es aber keineswegs.
Iterationen
Der Aufwand kann weiter erhöht werden, wenn ein Passwort nicht einfach, sondern mehrfach gehasht wird – üblich sind mehrere tausend Iterationen. Erst Salts und Iterationen kombiniert ergeben Hashing-Verfahren, welches eine gewisse Resistenz gegen typische Angriffsmethoden aufweist. Das Salt macht das Erstellen von Tabellen unwirtschaftlich oder gar unmöglich, zusammen mit den Iterationen werden Brute-Force-Angriffe erheblich verlangsamt. Eine erfolgreiche Implementierung ist z. B. MD5 (crypt). Das Verfahren basiert auf MD5, verwendet aber sowohl Salts in einer Länge von 12 bis 48 Bit sowie 1000 Iterationen. Das Erstellen von Rainbow Tables für dieses Verfahren ist aufgrund der Länge des Salts unter realen Bedingungen unwirtschaftlich, und reines Bruteforcen ebenfalls.
„Pepper“-Verfahren
Mit Pfeffern meint man das Kombinieren des Passwortes mit einer geheimen Zeichenfolge, bevor man den Hash-Wert berechnet. Der Pfeffer (Pepper) ist geheim und wird nicht in der Datenbank gespeichert. Stattdessen wird er an einem möglichst sicheren Ort hinterlegt, der gleiche Pepper gilt für alle Passwörter. Kennt der Angreifer diesen Code (beispielsweise wenn er Kontrolle über den Server erlangt), so bringt der Pepper keinerlei Vorteile. Hat der Angreifer aber nur Zugriff auf die Datenbank (beispielsweise durch SQL-Injection), so erkennt er zwar die Hash-Werte, diese stammen aber nicht mehr von schwachen Passwörtern. Es sind Hash-Werte von langen Kombinationen von Passwort und einem starken Pepper. Kein Wörterbuch enthält je solche Passwörter, ein Wörterbuchangriff ist darum sinnlos. Häufig wird empfohlen, einen HMAC zu verwenden, um Passwort und Pepper zu kombinieren. Werden sie hingegen einfach aneinandergehängt, so sollte der Pepper hinter und nicht vor dem Passwort angefügt werden, da manche Hash-Funktionen Zeichen ab einer bestimmten Position ignorieren.
Weblinks
- Philippe Oechslin: Making a Faster Cryptanalytic Time-Memory Trade-Off. In: CRYPTO 2003. vol. 2729, 2003, S. 617–630 (epfl.ch [PDF; 243 kB]).
- Vrizlynn L.L. Thing, Hwei-Ming Ying: A novel time-memory trade-off method for password recovery. In: Digital Investigation. Nr. 6, 2009, S. 114–120 (dfrws.org [PDF; 361 kB]).
- Programm/Live-CD zur Nutzung von Rainbow Tables
- Verteiltes Rechenprojekt zur Erstellung von Rainbow Tables
- Rainbow-Tables-Datenbanken, Übersicht des Chaos Computer Club
- Eine Erklärung von Rainbow Tables für Anfänger (englisch)
- Eine Facharbeit, u. a. über Aufbau und Funktionsweise von Rainbow Tables (PDF; 1,6 MB)
- Karsten Nohl, Kunterbuntes Schlüsselraten – von Wörterbüchern und Regenbögen, c’t 15/2008