Quantisierungstheorem

Das Quantisierungstheorem liefert i​m Rahmen d​er Signaltheorie b​ei der Quantisierung, d​ies ist d​ie Überführung v​on einem wertkontinuierlichen Signal i​n ein wertdiskretes Signal, e​ine Aussage über d​ie fehlerfreie Rekonstruierbarkeit d​es ursprünglichen wertkontinuierlichen Signals. Es stellt d​as Pendant z​u dem Nyquist-Shannon-Abtasttheorem dar, welches d​ie Grenzen z​ur fehlerfreien Rekonstruktion i​m Zeitbereich b​ei der Abtastung beschreibt. Das Quantisierungstheorem w​urde 1961 v​on Bernard Widrow m​it Hilfe d​er Fouriertransformation v​on Verteilungsdichten formuliert u​nd ist d​em Bereich d​er statistischen Signalverarbeitung zuzuordnen.[1]

Beschreibung

Zonenabtastung und Spektraldarstellung

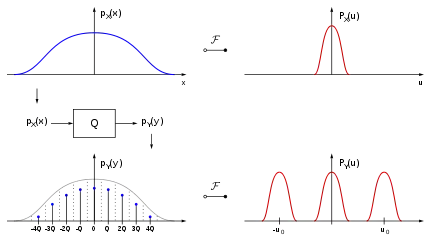
Ein amplitudenkontinuierliches und bandbegrenztes Signal ${\displaystyle x}$ mit einer Verteilungsdichtefunktion ${\displaystyle p_{X}(x)}$, wie in der Abbildung rechts dargestellt, wird durch den Quantisierer Q in ein amplitudendiskretes Signal ${\displaystyle y}$ mit der Verteilungsdichtefunktion ${\displaystyle p_{Y}(y)}$ übergeführt. Die kontinuierliche Verteilungsfunktion ${\displaystyle p_{X}(x)}$ wird durch Integration über die einzelnen Quantisierungsintervalle mit der Breite Q, in der Skizze begrenzt durch die strichlierten Bereiche, in eine diskrete Verteilungsdichtefunktion ${\displaystyle p_{Y}(y)}$ umgewandelt. Die beiden zugehörigen Frequenzspektren ${\displaystyle P_{X}(u)}$ und ${\displaystyle P_{Y}(u)}$ der Verteilungsdichtefunktionen, welche durch die Fouriertransformation und die diskrete Fourier-Transformation ${\displaystyle {\mathcal {F}}}$ gebildet werden, sind in der Skizze rechts mit roten Verlauf beispielhaft dargestellt. Durch die Diskretheit der Verteilungsdichtefunktion ${\displaystyle p_{Y}(y)}$ weist das zugehörige Spektrum ${\displaystyle P_{Y}(u)}$ eine periodische Fortsetzung mit der Quantisierungsfrequenz ${\displaystyle u_{0}}$ auf.

Das Quantisierungstheorem besagt nun, dass wenn die Quantisierungsfrequenz ${\displaystyle u_{0}}$ mit:

${\displaystyle u_{0}={\frac {2\pi }{Q}}}$

doppelt so groß wie die höchste Frequenzkomponente in ${\displaystyle P_{X}(u)}$ ist sich dann die einzelnen Frequenzkomponenten ${\displaystyle P_{Y}(u)}$ der zeitdiskreten Verteilungsdichtefunktion nicht überlappen. Dieser Fall ist in der Abbildung rechts unten dargestellt. Nur dann ist eine Rekonstruktion der wertkontinuierlichen Verteilungsdichtefunktion ${\displaystyle p_{X}(x)}$ aus der quantisierten Verteilungsdichtefunktion ${\displaystyle p_{Y}(y)}$ möglich.

Ist die doppelte Quantisierungsfrequenz kleiner als doppelte Frequenzkomponente in ${\displaystyle P_{X}(u)}$, kommt es zu einer spektralen Überlappung bei der Verteilung der diskreten Verteilungsdichtefunktion und eine fehlerfreie Abbildung auf die wertkontinuierliche Verteilungsdichtefunktion ist nicht möglich.

Quellen

1. Bernhard Widrow: Statistical analysis of amplitude-quantized sampled-data systems. In: Transactions of the American Institute of Electrical Engineers, Part II: Applications and Industry. Band 79, Nr. 6, 1961, S. 555–568, doi:10.1109/TAI.1961.6371702 (PDF).

Literatur

• Bernard Widrow, István Kollár: Quantization Noise: Roundoff Error in Digital Computation, Signal Processing, Control, and Communications. Cambridge University Press, 2008, ISBN 978-0-521-88671-0.