Pizza-Theorem

Das Pizza-Theorem ist ein mathematischer Satz in der ebenen Geometrie. Er beschreibt eine Flächengleichheit, die bei einer bestimmten Zerlegung des Kreises in Teilflächen entsteht.

8 Teile (n=0):
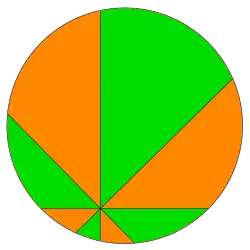
grüne Fläche (ungerade) = orange Fläche (gerade)

12 Teile (n=1):
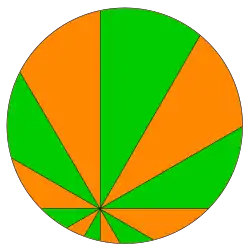
grüne Fläche (ungerade) = orange Fläche (gerade)

Legt man durch einen beliebigen inneren Punkt eines Kreises $4+2n$ Geraden ( $n\in \mathbb {N} _{0}$ ), so dass zwei benachbarte Geraden sich jeweils in einem Winkel von ${\frac {360^{\circ }}{2\cdot (4+2n)}}$ schneiden, dann erhält man eine Zerlegung des Kreises in $2\cdot (4+2n)$ Flächen. Nummeriert man diese nun im Uhrzeigersinn, so ist die Summe der Flächen mit geraden Nummern gleich der Summe der Flächen mit ungeraden Nummern.

Der Name des Theorems rührt von der Schnitttechnik her, mit der man üblicherweise eine runde Pizza in Stücke zerteilt. Setzt man das Messer statt am Mittelpunkt an irgendeinem anderen Punkt der Pizza an, so hat man genau die obige Situation.

Literatur

Wolfgang Kroll, Joachim Jäger: Das Pizzatheorem. (PDF) In: Mathematica Didactica, Jahrgang 33, 2010
Rick Mabry, Paul Deiermann: Of Cheese and Crust: A Proof of the Pizza Conjecture and Other Tasty Results. (PDF; 185 kB) In: The American Mathematical Monthly, Jahrgang 116, Nr. 5 (Mai, 2009), S. 423–438 (englisch) (JSTOR 40391118)
Larry Carter, Stan Wagon: Proof without Words: Fair Allocation of a Pizza. In: Mathematics Magazine, Vol. 67, No. 4 (Oct., 1994), S. 267

Weblinks

Commons: Pizza-Theorem – Sammlung von Bildern, Videos und Audiodateien

Eric W. Weisstein: Pizza Theorem. In: MathWorld (englisch).
Quellensammlung zum Pizza-Theorem (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.