Ossanna-Kreis
Der Ossanna-Kreis ist die Darstellung der Stromortskurve einer Drehstrom-Asynchronmaschine in der komplexen Ebene. Er ermöglicht eine relativ einfache Darstellung von Leistung, Drehmoment und Verlust einer Asynchronmaschine im Generator- und Motorbetrieb in Abhängigkeit vom Schlupf. Der Ossanna-Kreis gilt immer nur für den Betrieb einer Maschine mit einer Spannung, in der Regel der Nennspannung. Ändert sich die Spannung, so ändert sich der Durchmesser des Kreises.
Wird der Ständerwiderstand vernachlässigt, so ergibt sich eine vereinfachte Form, der Heyland-Kreis. Dieser gilt in erster Näherung und ist dadurch charakterisiert, dass die Drehmomentgerade mit der imaginären Achse zusammenfällt.
Dieses Kreisdiagramm der Asynchronmaschine wurde von Alexander Heyland im Jahr 1894 veröffentlicht und 1899 von Johann Ossanna in einer weiterentwickelten Form vorgestellt.
Die folgenden Bezeichnungen entsprechen denen in Bild "Ossanna-Kreis".
Ablesen der charakteristischen Werte
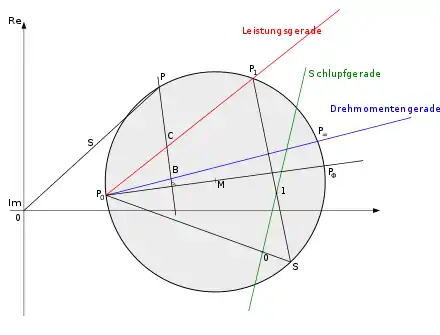
P0 bezeichnet den Leerlaufpunkt, P1 den realen Kurzschlusspunkt und P∞ den idealen Kurzschlusspunkt (Läuferwiderstand = 0). Der Durchmesser ist die Strecke zwischen P0 und PΦ. Die Leistungsgerade ist die Strecke zwischen P0 und P1. Die Drehmomentgerade zwischen P0 und P∞.
Jeder Zustand der Maschine ist ein Punkt auf dem Ossanna-Kreis. Wählt man solch einen Punkt P aus und fällt das Lot auf den Durchmesser, lassen sich sofort die Wirkleistung, das Drehmoment und die Verlustleistung bestimmen. Die Punkte B und C sind die Schnittpunkte mit der Drehmomentgeraden und der Leistungsgeraden. Die mechanische Wirkleistung Pm entspricht skaliert der Strecke zwischen den Punkten P und C. Die Strecke zwischen P und B entspricht dem Drehmoment. Die Strecke zwischen B und C beschreibt die in der Läuferwicklung entstehende Verluste.
Konstruktion des Kreises
Sind die komplexen Ströme von drei Arbeitspunkten der Maschine bekannt, so lässt sich der Kreis geometrisch aus diesen bestimmen.
Der Schlupf für jeden Punkt lässt sich mittels einer Schlupfgeraden bestimmen. Diese wird konstruiert, indem von einem beliebigen Punkt S auf dem Kreis eine Verbindung zu P∞ gezogen wird. Eine beliebige zu dieser Verbindung parallele Gerade kann als Schlupfgerade genutzt werden. Die Achsenskalierung ergibt sich aus dem Punkt "0" (Schnittpunkt der Strecke zwischen P0 und S mit der Schlupfgeraden) und dem Punkt "1" (Schnittpunkt der Strecke zwischen P1 und S mit der Schlupfgeraden). Ansonsten ist die Schlupfgerade durch eine lineare Skala charakterisiert. Um von einem beliebigen Punkt P den Schlupf zu bestimmen muss zwischen P und S eine Gerade gezogen werden, deren Schnittpunkt mit der Schlupfgeraden auf ihrer Skala den Schlupf ergibt.
Literatur
Eckhard Spring: Elektrische Maschinen, Springer-Lehrbuch, 2006 (ISBN 9783540282419)