Netze in Netzen (Petrinetze)
Netze in Netzen sind ein Modellierungsansatz aus der Petri-Netz-Familie.
Von anderen Arten von Petrinetzen heben sie sich durch die Möglichkeit ab, Marken mit einer inneren Struktur zu versehen, die ihrerseits wieder auf Petrinetzbasis funktioniert. Ein Netz kann also weitere Netzexemplare enthalten, die in ihm umherbewegt werden und dabei selbst schalten können.
Motivation
Netze in Netzen eignen sich[1] zur Modellierung verteilter Systeme mit besonderem Augenmerk auf Aspekte der
- Hierarchie,
- Mobilität und
- Kapselung
Bei vielen Entwicklungen wurde absichtlich ein starker Bezug zur Objektorientierung gesucht, um die Fähigkeit der Petrinetze, nebenläufige Verarbeitung zu modellieren, zu verbinden mit dem Modellieren mit Objekten, die erzeugt werden können und interagieren.
Geschichte
Ausgehend von Anforderungen aus der Praxis sind seit Mitte der 90er Jahre verschiedene Formalismen entwickelt worden, auf die die Beschreibung "Netze in Netzen" passt. Lomazova und Schnoebelen[2] listen in dem genannten Artikel einige auf, die allgemein bekannt sind: Sibertin-Blanc,[3] Lakos,[4] Moldt und Wienberg[5] als auf Gefärbte Petrinetze aufbauend, daneben die Objektnetze von Valk.[6]
Die früheste Verwendung hierarchischer Netzmodelle findet sich bei Valk und Jessen[7], wo Valk in einem Beitrag die sogenannten "Task/Flow Nets"[8] einführte, um Auftragssysteme kompakt modellieren zu können. In diesen Modellen laufen Aufträge als Marken durch ein Netz, das ihre Abarbeitung modelliert; zugleich haben die einzelnen Aufträge jeweils einen inneren Status, der ihre Geschichte speichert und anzeigt, inwieweit sie schon abgearbeitet wurden.
Semantiken
Die hauptsächliche Unterscheidung in der Interpretation findet bei der Behandlung der Marken statt. Sind Marken lediglich Referenzen auf Netzexemplare, die in einem gegebenen globalen Zustand nebeneinander existieren, so handelt es sich um eine Referenzsemantik, sind Marken dagegen selbst als Netze zu interpretieren, so liegt eine Wertesemantik vor. Diese unterscheiden sich in der Behandlung von gleichartigen Marken: Netzmarken in der Wertsemantik existieren unabhängig voneinander und haben jeweils eigene Zustände.
Ein Problem ergibt sich noch nicht unbedingt beim Kopieren, spätestens aber beim Zusammenführen verschiedener Exemplare "desselben" Netzes. Bisweilen ist hier eine dritte Art von Semantik, die in dem Artikel[9] vorgeschlagen worden ist, sinnvoll. Bei dieser Abart der Wertsemantik werden die Ablaufgeschichten der Exemplare zur kleinsten Ablaufgeschichte zusammengeführt, die beide beinhaltet.
Auch sind Mischformen möglich und mitunter modellierungstechnisch relevant.[10]
Kommunikation
Ohne Kommunikation zwischen den Netzexemplaren lässt sich recht wenig modellieren; wie in der objektorientierten Programmierung bieten die Formalismen daher in der Regel eine Kommunikation der Objekte (Netzexemplare) über vorher festgelegte Schnittstellen an, die allerdings dynamisch gebunden werden.
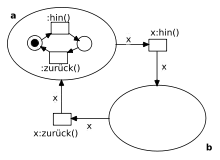
Abbildung 1 zeigt ein Beispiel für ein Netz, das ein anderes Netz enthält. Dieses Beispiel ist so einfach gestaltet, dass Wert- und Referenzsemantik zusammenfallen. Das innere Netz ist beweglich und kann als Marke von Ort "a" zu Ort "b" geschaltet werden; die Kanalanschriften wirken hier wie Methodenaufrufe und sorgen dafür, dass sich dieser äußere Zustand nach dem synchronisierten Schalten der "aufrufenden" und der "aufgerufenen" Transition im inneren Netz widerspiegelt. Das "x" an den Kanten ist eine Variable, die beim Schalten einer Transition des äußeren Netzes an die Netzmarke gebunden wird.
Algorithmen und eingeschränkte Formalismen
Klassische Petrinetz-Eigenschaften wie Erreichbarkeit, Beschränktheit und Lebendigkeit sind nur teilweise entscheidbar. Die Arbeit[11] von Köhler-Bußmeier gibt einen Überblick über Entscheidbarkeitsfragen bei elementaren Objekt-Netzen. Um die Komplexität zu reduzieren wurden Unterklassen definiert, indem die Struktur der unterliegenden Petrinetze eingeschränkt wurde, wie zum Beispiel als Zustands-Maschine. Solche Einschränkungen erlauben immer noch die komplexe Modellierung von z. B. mobilen Systemen, haben aber polynomielle Komplexität beim Model Checking[12].
Werkzeuge
- CO-OPN https://smv.unige.ch//research-projects/co-opn basiert auf Algebraischen Höheren Netzen
- RENEW http://www.renew.de ist eine freie Entwicklungsumgebung für Referenznetze mit Java-Integration[13]
Literaturverweise
- Michael Köhler-Bußmeier: Objektnetze: Definition und Eigenschaften, Logos-Verlag, Berlin, 2004
- Irina A. Lomazova und Philippe Schnoebelen: Some decidability results for nested Petri nets, Perspectives of System Informatics, pp. 208–220, Springer 2000
- C. Sibertin-Blanc: Cooperative nets, Application and Theory of Petri Nets 1994, pp. 471–490, Springer 1994
- Charles Lakos: From coloured Petri nets to object Petri nets, Application and Theory of Petri Nets 1995, pp 278--297, 1995, Springer
- Daniel Moldt und Frank Wienberg: Multi-agent-systems based on coloured Petri nets, Application and Theory of Petri Nets 1997, pp. 82–101, Springer 1997
- Rüdiger Valk: Petri nets as token objects, Application and Theory of Petri-Nets, pp. 1–24, Springer, 1998
- Eike Jessen, Rudiger Valk: Rechensysteme: Grundlagen der Modellbildung, Studienreihe Informatik, 1987, Springer, Heidelberg
- Rüdiger Valk: Object Petri Nets, Lectures on Concurrency and Petri Nets, p. 819–848, Springer 2004
- Rüdiger Valk: Object Petri Nets, Lectures on Concurrency and Petri Nets, pp. 819–848, Springer 2004
- Berndt Farwer und Michael Köhler: Modelling global and local name spaces for mobile agents using object nets, Fundamenta Informaticae, Vol. 72, No 1, pp. 109–122, IOS Press 2006
- Michael Köhler-Bußmeier: A Survey of Decidability Results for Elementary Object Systems: Fundamenta Informaticae, Vol. 130, No 1, pp. 99–123, 2014
- Frank Heitmann, Michael Köhler-Bußmeier: P- and t-systems in the nets-within-nets formalism: Springer LNCS 7347, 2012, pp. 368–387
- Olaf Kummer: Referenznetze, Dissertation, Universität Hamburg, Logos Verlag Berlin 2002