Morley-Dreieck
Das Morley-Dreieck, benannt nach Frank Morley, ist ein gleichseitiges Dreieck, welches innerhalb eines beliebigen Dreiecks konstruiert werden kann.
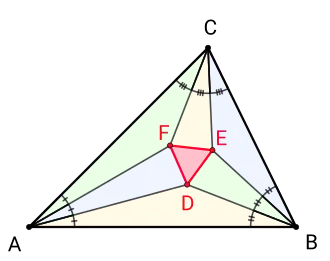
Morley-Dreieck DEF (rot)
Definition und Satz von Morley
Die Innenwinkel eines beliebigen Dreiecks werden jeweils in drei gleich große Winkel unterteilt (was im Allgemeinen mit Zirkel und Lineal nicht möglich ist). Zu jeder Dreiecksseite betrachtet man den Schnittpunkt derjenigen zwei Teilungslinien, die von den Endpunkten dieser Seite ausgehen und zu dieser Seite benachbart sind. Das Morley-Dreieck ist dasjenige Dreieck, dessen Ecken die drei auf diese Weise erhaltenen Schnittpunkte sind.
Der Satz von Morley lautet:[1] Unabhängig von der Form des ursprünglichen Dreiecks ist das Morley-Dreieck stets gleichseitig.
Siehe auch
Literatur
- H. S. M. Coxeter, S. L. Greitzer: Zeitlose Geometrie. Klett, Stuttgart 1983.
- Horst Hischer: Grundlegende Begriffe der Mathematik: Entstehung und Entwicklung: Struktur – Funktion – Zahl. Springer 2012, ISBN 9783834886323, S. 2–4
- Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: Mit harmonischen Verhältnissen zu Kegelschnitten: Perlen der klassischen Geometrie. Springer 2016, ISBN 9783662530344, S. 182–185
- Martin Erickson: Mathematische Appetithäppchen: Faszinierende Bilder. Packende Formeln. Reizvolle Sätze. Springer, 2015, ISBN 9783662454596, S. 60–63 (mit Conways elegantem Beweis)
Weblinks
- Morley's Miracle - Satz, Illustration und Hintergrundinformationen sowie 26 verschiedene Beweise auf cut-the-knot.org
- Florian Modler: Vergessene Sätze am Dreieck. Teil 8: Der Schmetterling und der Satz von Morley. In: Matroids Matheplanet.
- Eric W. Weisstein: Morley’s Theorem. In: MathWorld (englisch).
- Eric W. Weisstein: First Morley Triangle. In: MathWorld (englisch).
- Rudolf Fritsch: Ein einfacher Beweis des Satzes von Morley. (PDF; 70 kB, archivierte Version)
Einzelnachweise
- Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3, S. 131
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.