Minimale verbundene Gewinnkoalition
Eine minimale verbundene Gewinnkoalition (minimal connected winning coalition) ist eine Koalition von Parteien, die politisch zusammenhängend sind und eine Mehrheit im Parlament erlangen, bei der alle Parteien benötigt werden. Die zugehörige Theorie wurde 1970 von Robert Axelrod formuliert. Unter der Annahme, dass sich Parteien bei der Suche nach Koalitionspartnern sowohl daran orientieren, wie viele Ämter sie in einer potenziellen Koalitionsregierung besetzen können, als auch daran interessiert sind, mit Parteien zusammen zu regieren, die ihnen programmatisch bzw. ideologisch nahestehen, beinhaltet Axelrods Konzept Elemente sowohl ämter- als auch policy-orientierter Koalitionstheorien.
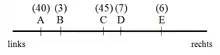
Voraussetzung für die Anwendung der Theorie ist die Plausibilität, alle Parteien ordnen zu können, z. B. auf einer eindimensionalen Links-Rechts-Achse wie in dem angezeigten Beispiel mit den Parteien A, B, C, D und E.
Definition
Eine Koalition heißt dann verbunden, wenn alle Parteien zwischen der linkesten und rechtesten Koalitionspartei ebenfalls Mitglied der Koalition sind. Ein Bündnis aus A, B und C wäre somit eine verbundene Koalition, die Koalition aus B, D und E hingegen nicht (weil die zwischen B und D liegende Partei C nicht Teil der Koalition ist).
Zweitens ist von Bedeutung, ob eine mögliche Koalition über die Mehrheit der Sitze verfügt oder nicht. Falls dies der Fall ist, wird sie als Gewinnkoalition bezeichnet. Geht man von einem Parlament mit 101 Sitzen aus, bei dem die Mehrheit ab 51 Sitzen erreicht wird, so wäre in der Beispielabbildung z. B. die Koalition {C, D} mit 52 Sitzen eine Gewinnkoalition, die Koalition {A, B} mit 43 Sitzen nicht.
Eine verbundene Gewinnkoalition ist dann eine Koalition, die beide Kriterien erfüllt, die also sowohl verbunden im Sinne der obigen Definition ist als auch mehr als 50 % der Sitze auf sich vereinen kann. Beispielsweise wäre die Koalition {A, B, C, D} eine verbundene Gewinnkoalition. Keine verbundenen Gewinnkoalitionen sind hingegen {D, E} – weil ohne Mehrheit – oder {A, C} – weil nicht verbunden.
Als minimale verbundene Gewinnkoalition wird eine verbundene Gewinnkoalition dann bezeichnet, wenn jede einzelne an ihr beteiligte Partei benötigt wird, um den Status als verbundene Gewinnkoalition zu erreichen. Anders ausgedrückt: Durch den Austritt einer beliebigen Partei wäre die Koalition keine Gewinnkoalition mehr oder nicht mehr verbunden (oder beides).
In dem Beispiel hier ist {A, B, C} eine minimale verbundene Gewinnkoalition. Die Parteien A und C sind beide für den Mehrheitsstatus der Koalition nötig, Partei B für die Verbundenheit. Die Koalition {C, D, E} hingegen ist keine minimale verbundene Gewinnkoalition. Partei E ist insofern überflüssig, als sie weder zum Erreichen der Mehrheit noch der Verbundenheit benötigt wird. Würde Sie die Koalition verlassen, wäre die verbleibende Koalition {C, D} immer noch eine verbundene Gewinnkoalition.
Implikationen
Dadurch, dass Parteien in minimalen verbundenen Gewinnkoalitionen einseitig für den Mehrheitserhalt benötigt werden können, beinhaltet die Theorie das Element der Ämterorientierung. Andererseits können Parteien auch ausschließlich die Verbundenheit der Koalition sichern, ohne zum Erhalt der Mehrheit etwas beizutragen. Hieran zeigt sich die Policy-Komponente.
Axelrods Konzept ist keine Verfeinerung der Theorie der minimalen Gewinnkoalitionen in dem Sinne, dass alle minimalen verbundenen Gewinnkoalitionen auch minimale Gewinnkoalitionen sein müssen. Das obige Beispiel der Koalition {A, B, C} stellt ein Gegenbeispiel dar.
Quellen
- Axelrod, Robert (1970): Conflict of Interest: A Theory of Divergent Goals with Application to Politics. Chicago: Markham.
- Linhart, Eric (2014): Räumliche Modelle der Politik: Einführung und Überblick. In: Linhart, Eric, Kittel, Bernhard & Bächtiger, André (Hrsg.), Jahrbuch für Handlungs- und Entscheidungstheorie, Band 8. Wiesbaden: Springer VS, S. 3–44.
- Saalfeld, Thomas (2007): Parteien und Wahlen. Baden-Baden: Nomos.