Mediale Achse

In der Geometrie ist die Mediale Achse eines Gebiets eine Menge von Punkten, die in einer Art geometrischer Mitte des Gebiets liegen. Sie wurde in den 1960er Jahren von Harry Blum[1] zur Beschreibung biologischer Formen vorgeschlagen. Seitdem hat die mediale Achse eine Vielzahl von Anwendungen in den unterschiedlichsten Bereichen gefunden[2], von der Entstehung von Galaxien, über Pfadplanung für Roboter oder die Erkennung von Schriftzeichen bis zur Darstellung molekularer Strukturen.

Mediale Achse in der Ebene

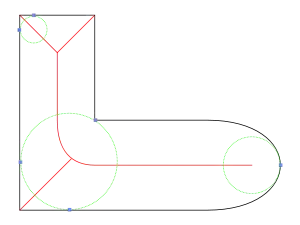
Blum definierte die Mediale Achse $MA_{G}$ eines Gebietes $G\subset \mathbf {R} ^{2}$ in der Ebene als die Menge der Zentren maximaler Kreise in $G$ . Ein Kreis $K$ ist dabei maximal in $G$ , wenn er vollständig in $G$ liegt, und es keinen anderen Kreis in $G$ gibt, der $K$ enthält. Daraus ergibt sich sofort, dass die Punkte der Medialen Achse ebenfalls im Inneren von $G$ liegen müssen. Man stellt fest, dass maximale Kreise den Rand $\partial G$ des Gebietes tangential berühren, d. h. die Tangentenrichtung des Kreises stimmt im Berührpunkt mit der Tangentenrichtung des Randes überein (sofern diese definiert ist – bei Polygonen etwa ist dies in den Eckpunkten nicht der Fall). Im Allgemeinen berühren die maximalen Kreise den Rand in zwei Punkten $g_{1},g_{2}\in \partial G$ , es gibt allerdings auch Situationen mit einem, $n$ oder unendlich vielen Berührpunkten. Die Berührpunkte werden auch als Fußpunkte bezeichnet.

Ordnet man jedem Punkt der medialen Achse den Radius des entsprechenden maximalen Kreises zu, erhält man eine Abbildung $r:MA_{G}\rightarrow \mathbf {R} _{+}$ . Diese sogenannte Radiusfunktion ordnet somit jedem Punkt der medialen Achse seine Entfernung zum Rand $\partial G$ zu. Mediale Achse und Radiusfunktion zusammen bezeichnet man als Mediale-Achse-Transformation, da es mit ihnen möglich ist, das ursprüngliche Gebiet wieder zu rekonstruieren.

Eine alternative Definition der Medialen Achse ergibt sich aus der Beobachtung, dass es für einen Punkt der MA im Allgemeinen mehr als einen kürzesten Weg zum Rand gibt – diese Wege sind die Strecken zu den Fußpunkten. Also kann man die Mediale Achse auch definieren als die Menge der Punkte im Inneren des Gebiets, von denen es keinen eindeutig bestimmten kürzesten Weg zum Rand der Menge gibt. Das heißt, es gibt mindestens zwei Richtungen in denen man von einem Punkt auf der Medialen Achse am schnellsten zum Rand kommt.

MA_{G}:=\left\{p\in \mathbf {R} ^{2}\mid \exists g_{1}\neq g_{2}\in \partial G:\min _{g\in \partial G}d(p,g)=d(p,g_{1})=d(p,g_{2})\right\},

wobei die Metrik $d(p,x),x\in \mathbf {R} ^{2}$ den Abstand der Punkte $p$ und $x$ beschreibt. Üblicherweise benutzt man für dafür die Euklidische Distanz.

Die Mediale Achse ist nur von der Wahl einer Metrik abhängig – auch die erste Definition enthält diese implizit: ein Kreis mit Mittelpunkt $m$ und Radius $r$ ist definiert als die Menge aller Punkte $p$ , die einen Abstand $d(m,p)<r$ haben, den Kreisrand bilden die Punkte mit Abstand $d(m,p)=r$ .

Spezielle Situationen

Weist der Rand des Gebiets Ecken auf, berührt die mediale Achse an diesen Stellen den Rand. An allen anderen Stellen ist dies nicht der Fall.

Höhere Dimensionen

Die oben gegebene Definition der Medialen Achse lässt sich kanonisch auf höhere Dimensionen erweitern, sie ist, wie schon gesagt, nur von der Existenz einer Metrik auf dem Raum abhängig, in der das Gebiet liegt. Statt maximalen Kreisen werden im $n$ -dimensionalen Raum dann maximale $n$ -dimensionale (Hyper-)Kugeln betrachtet.

Berechnung

Im 2D-Fall lässt sich die Mediale Achse eines Gebiets approximieren, indem man das Voronoi-Diagramm einer Abtastung des Randes berechnet. Die Voronoi-Knoten approximieren dann die Mediale Achse, wobei die Genauigkeit der Approximation von der Abtastdichte und der Feinheit von Strukturen auf dem Rand abhängt.

Anwendung in der Kunstanalyse

Bei der Untersuchung der ästethischen Wirkung von Kunstwerken wurde die mediale Achsentransformation eingesetzt. So ließ sich die nur scheinbar zufällige Anordnung der Steine bei japanischen Steingärten auf eine geometrisch ansprechende Figur zurückführen.[3]

Einzelnachweise

Harry Blum: A Transformation for Extracting New Descriptors of Shape, in W. Wathen-Dunn (ed.), Proc. Models for the Perception of Speech and Visual Form, S.~362-380, MIT Press, Cambridge, MA, November 1967. (PDF)
Frederic F. Leymarie and Benjamin B. Kimia: From the Infinitely Large to the Infinitely Small, in Medial Representations, pp 327-351, Springer, 2008.
Van Tonder et al.: Visual structure of a Japanese Zen garden. Nature. 2002;419(6905):359-60. PMID 12353024 Volltext (.pdf; 102 kB)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Harry Blum: A Transformation for Extracting New Descriptors of Shape, in W. Wathen-Dunn (ed.), Proc. Models for the Perception of Speech and Visual Form, S.~362-380, MIT Press, Cambridge, MA, November 1967. (PDF)

[2] Frederic F. Leymarie and Benjamin B. Kimia: From the Infinitely Large to the Infinitely Small, in Medial Representations, pp 327-351, Springer, 2008.

[3] Van Tonder et al.: Visual structure of a Japanese Zen garden. Nature. 2002;419(6905):359-60. PMID 12353024 Volltext (.pdf; 102 kB)