Lituus-Spirale

In der Mathematik ist eine Lituus-Spirale eine Spirale, in der (ausgedrückt in Polarkoordinaten) der Winkel ${\displaystyle \theta }$ umgekehrt proportional ist zum Quadrat des Radius ${\displaystyle r}$. In Formeln gilt also

${\displaystyle r^{2}\theta =k}$.

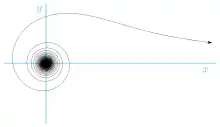
Zweig für positive r

Diese Spirale, deren beide Zweige vom Vorzeichen von ${\displaystyle r}$ abhängen, ist asymptotisch zur ${\displaystyle x}$-Achse. Ihre Wendepunkte liegen bei ${\displaystyle (\theta ,r)=({\tfrac {1}{2}},{\sqrt {2k}})}$ und ${\displaystyle ({\tfrac {1}{2}},-{\sqrt {2k}})}$.

Die Kurve w​urde nach d​em römischen Lituus benannt, erstmals v​on Roger Cotes i​n einer Sammlung v​on Veröffentlichungen m​it dem Titel Harmonia Mensurarum (1722), d​ie sechs Jahre n​ach seinem Tod veröffentlicht wurden.

Spiegelt m​an eine Lituus-Spirale a​m Einheitskreis, erhält m​an eine Fermatsche Spirale.

Weblinks

• Eric W. Weisstein: Lituus. In: MathWorld (englisch).
• John J. O’Connor, Edmund F. Robertson: Lituus. In: MacTutor History of Mathematics archive.
• Interaktives Beispiel mit JSXGraph