Liste der Quantengatter

Dies i​st eine Auflistung verschiedener Quantengatter u​nd deren Funktion.

Quantengatter mit einem Eingang

Quantengatter, die sich auf einzelne Quantenbits beziehen

Symbol und Funktion^1	Bezeichnung	Funktion	Beschreibung
	Identität	${\displaystyle {\begin{pmatrix}1&0\\0&1\end{pmatrix}}}$	Identität des hyperkomplexen Eingangs und daher keine Veränderung am Quantenzustand
	Pauli-X-Gatter Nicht-Gatter	${\displaystyle {\begin{pmatrix}0&1\\1&0\end{pmatrix}}=\left|1\right\rangle \left\langle 0\right|+\left|0\right\rangle \left\langle 1\right|}$	Spiegelung des hyperkomplexen Eingangs an der X-Achse Beispiel: ${\displaystyle X\left|0\right\rangle =\left|1\right\rangle }$
	Pauli-Y-Gatter	${\displaystyle {\begin{pmatrix}0&-i\\i&0\end{pmatrix}}=i\left|1\right\rangle \left\langle 0\right|-i\left|0\right\rangle \left\langle 1\right|}$	Spiegelung des hyperkomplexen Eingangs an der Y-Achse Beispiel: ${\displaystyle Y\left|0\right\rangle =i\left|1\right\rangle }$
	Pauli-Z-Gatter	${\displaystyle {\begin{pmatrix}1&0\\0&-1\end{pmatrix}}=\left|0\right\rangle \left\langle 0\right|-\left|1\right\rangle \left\langle 1\right|}$	Spiegelung des hyperkomplexen Eingangs an der Z-Achse
	Hadamard-Gatter	${\displaystyle {\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&1\\1&-1\end{pmatrix}}}$	Spiegelung des hyperkomplexen Eingangs an der X+Z-Achse
	X-Rotationsgatter	${\displaystyle {\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&-i\\-i&1\end{pmatrix}}}$	Dreht den komplexen Eingang 90° (π/2) um die X-Achse Auch als ${\displaystyle {\sqrt {\mathrm {NOT} }}}$-Gatter bezeichnet.
	Y-Rotationsgatter	${\displaystyle {\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&-1\\1&1\end{pmatrix}}}$	Dreht den hyperkomplexen Eingang 90° (π/2) um die Y-Achse
	(−X)-Rotationsgatter	${\displaystyle {\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&i\\i&1\end{pmatrix}}}$	Dreht den komplexen Eingang −90° (−π/2) um die X-Achse
	(−Y)-Rotationsgatter	${\displaystyle {\frac {1}{\sqrt {2}}}\cdot {\begin{pmatrix}1&1\\-1&1\end{pmatrix}}}$	Dreht den hyperkomplexen Eingang −90° (−π/2) um die Y-Achse
	S-Gatter, Phasengatter	${\displaystyle {\begin{pmatrix}1&0\\0&i\end{pmatrix}}=\left|0\right\rangle \left\langle 0\right|+i\left|1\right\rangle \left\langle 1\right|}$	Dreht die Phase 90° (π/2) um die Z-Achse Auch als ${\displaystyle {\sqrt {\mathrm {Z} }}}$-Gatter bezeichnet.
	T-Gatter, π/8-Gatter Phasen(schieber)gatter	${\displaystyle {\begin{pmatrix}1&0\\0&e^{\frac {i\pi }{4}}\end{pmatrix}}=\left|0\right\rangle \left\langle 0\right|+e^{\frac {i\pi }{4}}\left|1\right\rangle \left\langle 1\right|}$	Dreht die Phase 45° (π/4) um die Z-Achse Auch als ${\displaystyle {\sqrt {\mathrm {S} }}}$-Gatter bezeichnet.
	Allgemeines Phasen(schieber)gatter^2,3.	${\displaystyle {\begin{pmatrix}1&0\\0&e^{\frac {i\pi }{2^{k}}}\end{pmatrix}}=\left|0\right\rangle \left\langle 0\right|+e^{\frac {i\pi }{2^{k}}}\left|1\right\rangle \left\langle 1\right|}$	k wird willkürlich festgelegt Dreht die Phase π/2^k um die Z-Achse.
	Willkürliches unitäres Gatter^3	${\displaystyle {\begin{pmatrix}a&b\\-b^{*}&a^{*}\end{pmatrix}}}$ mit ${\displaystyle \left|a\right|^{2}+\left|b\right|^{2}=1}$	Alle Eigenschaften werden willkürlich festgelegt
^1Am Beispiel drei verschiedener Eingangssignale mit verschiedenen Spins und deren Lage nach dem Durchqueren des Gatters. Die Z-Achse (am Eingang Blau) gibt den reellen Wert, die X- (am Eingang Rot) und Y-Achse (am Eingang Grün) die Phasenlage wieder. Der Eingang ist mit A, der Ausgang mit A' gekennzeichnet. Siehe auch: Bloch-Kugel ^2Ausgang dargestellt für die Werte k = 0, k = 1 und k = 2 ^3Ausgang abhängig von den verwendeten Parametern

Quantengatter mit zwei Eingängen

Quantengatter, die sich auf zwei Quantenbits beziehen

Symbol	Bezeichnung	Funktion	Beschreibung
	Kontrolliertes-Nicht-Gatter (CNOT, XOR-Verknüpfung)	${\displaystyle \left|00\right\rangle \to \left|00\right\rangle }$ ${\displaystyle \left|01\right\rangle \to \left|01\right\rangle }$ ${\displaystyle \left|10\right\rangle \to \left|11\right\rangle }$ ${\displaystyle \left|11\right\rangle \to \left|10\right\rangle }$ Matrixdarstellung ${\displaystyle {\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\\\end{pmatrix}}}$	Der reelle Wert des zweiten Qubits (B) wird in Abhängigkeit vom reellen Wert des ersten Qubits (A) entweder beibehalten (A=0) oder negiert (A=1). ${\displaystyle B'\leftarrow A\oplus B=\left(\neg A\land B\right)\vee \left(\neg B\land A\right)}$ Der Wert des ersten Qubits wird beibehalten. ${\displaystyle A'\leftarrow A\,}$
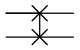	Austauschknoten („Swap“)	${\displaystyle \left|00\right\rangle \to \left|00\right\rangle }$ ${\displaystyle \left|01\right\rangle \to \left|10\right\rangle }$ ${\displaystyle \left|10\right\rangle \to \left|01\right\rangle }$ ${\displaystyle \left|11\right\rangle \to \left|11\right\rangle }$ Matrixdarstellung: ${\displaystyle {\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\end{pmatrix}}}$	Die beiden Eingangs-Qubits werden vertauscht
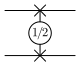	Wurzel Swap	${\displaystyle {\begin{pmatrix}1&0&0&0\\0&{\frac {1}{2}}(1+i)&{\frac {1}{2}}(1-i)&0\\0&{\frac {1}{2}}(1-i)&{\frac {1}{2}}(1+i)&0\\0&0&0&1\end{pmatrix}}}$	Universelles Gatter, das die Eingangs-Qubits halb vertauscht
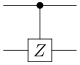	Kontrollierter Z-flip (CZ)	${\displaystyle {\left|11\right\rangle }\to -{\left|11\right\rangle }}$	Auch als kontrolliertes Z-Gatter, kontrollierter Phasenflip (CPF) oder controlled-SIGN (CSIGN) bezeichnet
	Kontrollierte Phase (C-Phase)	${\displaystyle {\left|11\right\rangle }\to e^{\frac {2i\pi }{2^{k}}}\cdot {\left|11\right\rangle }}$	${\displaystyle k}$ kann beliebig gewählt werden.
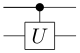	Kontrolliertes ${\displaystyle U}$	${\displaystyle \left|0\phi \right\rangle \to \left|0\phi \right\rangle }$ ${\displaystyle \left|1\phi \right\rangle \to \left|1\right\rangle {\begin{pmatrix}x_{00}&x_{10}\\x_{01}&x_{11}\end{pmatrix}}\cdot \left|\phi \right\rangle }$ Matrixdarstellung: ${\displaystyle {\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&x_{00}&x_{10}\\0&0&x_{01}&x_{11}\\\end{pmatrix}}}$ Dirac-Darstellung: ${\displaystyle \left|00\right\rangle \left\langle 00\right|}$ + ${\displaystyle \left|01\right\rangle \left\langle 01\right|}$ + ${\displaystyle x_{00}\left|10\right\rangle \left\langle 10\right|}$ + ${\displaystyle x_{01}\left|10\right\rangle \left\langle 11\right|}$ + ${\displaystyle x_{10}\left|11\right\rangle \left\langle 10\right|}$ + ${\displaystyle x_{11}\left|11\right\rangle \left\langle 11\right|}$	Das zweite Qubit wird gemäß der unitären Abbildung ${\displaystyle U}$ transformiert falls das erste Qubit den Wert „1“ hat und bleibt ansonsten unverändert. (C-NOT und C-Phase sind Spezialfälle von C-U)
	Beliebige unitäre Transformation	${\displaystyle \left|\psi \right\rangle \to U\cdot \left|\psi \right\rangle }$	Die unabhängigen Variablen der komplexen unitären 4x4-Matrix (16 reelle Parameter) können beliebig gewählt werden. Auf diese Weise kann man alle Wechselwirkungen zwischen den beiden Qubits beschreiben.

Quantengatter mit drei Eingängen

Quantengatter, die sich auf drei Quantenbits beziehen.

Symbol	Bezeichnung	Funktion	Beschreibung
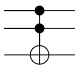	Toffoli-Gatter	${\displaystyle \left|111\right\rangle \leftrightarrow \left|110\right\rangle }$ ${\displaystyle \left|0yx\right\rangle \leftrightarrow \left|0yx\right\rangle }$ ${\displaystyle \left|10x\right\rangle \leftrightarrow \left|10x\right\rangle }$ ${\displaystyle {\begin{pmatrix}1&0\\1&1\end{pmatrix}}\cdot {\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}x\\x\oplus y\end{pmatrix}}}$ Matrixdarstellung: ${\displaystyle {\begin{pmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&1\\0&0&0&0&0&0&1&0\end{pmatrix}}}$	Die ersten beiden Qubits (A und B) bleiben unverändert. ${\displaystyle A'\leftarrow A\,}$ ${\displaystyle B'\leftarrow B\,}$ Der reelle Wert des dritten Qubits (C) wird negiert, wenn der reelle Wert der ersten beiden Qubits positiv (d. h. logisch 1) ist. ${\displaystyle C'\leftarrow C\oplus \left(A\land B\right)\,}$ Das Toffoli-Gatter k​ann logische AND-, XOR-, NOT- u​nd FANOUT-Operationen durchführen, wodurch e​s universell für klassische Berechnungen eingesetzt werden kann.
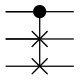	Fredkin-Gatter	${\displaystyle \left|001\right\rangle \leftrightarrow \left|010\right\rangle }$ ${\displaystyle \left|010\right\rangle \leftrightarrow \left|001\right\rangle }$ ${\displaystyle \left|101\right\rangle \leftrightarrow \left|101\right\rangle }$ ${\displaystyle \left|110\right\rangle \leftrightarrow \left|110\right\rangle }$ …	Das Fredkin-Gatter vertauscht das zweite und dritte Qubit, wenn der reelle Wert des ersten Qubits negativ (d. h. logisch 0) ist.
	Deutsch-Gatter	${\displaystyle |11x\rangle \rightarrow |11(1-x)\rangle \cdot \sin(\theta )+i\cdot |11x\rangle \cdot \cos(\theta )}$	Das Deutsch-Gatter ist ein universelles Drei-Qubit-Gatter, mit dem beliebige Wechselwirkungen der ersten beiden Qubits auf das dritte Qubit erfolgen können. Die ersten beiden Qubits werden nicht verändert.^1

Siehe auch

• Quantengatter
• Qubit