Iterierter Logarithmus

Der iterierte Logarithmus einer positiven Zahl n, bezeichnet mit ${\displaystyle \log ^{*}n}$ (gesprochen „log Stern von n“), gibt an, wie oft die Logarithmusfunktion anzuwenden ist, damit das Ergebnis kleiner oder gleich 1 ist.

Definition

Formal ist die Iterierte logarithmische Funktion, die jeder positiven Zahl ihren iterierten Logarithmus zuordnet, wie folgt rekursiv definiert:

${\displaystyle \log ^{*}n:={\begin{cases}0&{\mbox{falls }}n\leq 1;\\1+\log ^{*}(\log n)&{\mbox{falls }}n>1\end{cases}}}$

Wird 2 als Basis des Logarithmus verwendet, schreibt man den iterierten Logarithmus auch als ${\displaystyle \lg ^{*}n}$.

Beispiele

Abb. 1: Beispiel für lg* 4 = 2

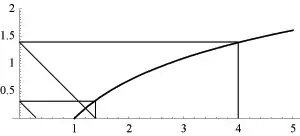
Graphisch kann die Bestimmung des iterierten Logarithmus einer Zahl bestimmt werden durch die Anzahl der Schleifen, die gemäß dem Beispiel in Abb. 1 benötigt werden, um das Intervall [0, 1] auf der ${\displaystyle x}$-Achse zu erreichen.

Der iterierte Logarithmus ist eine sehr langsam steigende Funktion:

${\displaystyle x}$	${\displaystyle \lg ^{*}x}$
${\displaystyle (-\infty ,1]}$	${\displaystyle 0}$
${\displaystyle (1,2]}$	${\displaystyle 1}$
${\displaystyle (2,4]}$	${\displaystyle 2}$
${\displaystyle (4,16]}$	${\displaystyle 3}$
${\displaystyle (16,65536]}$	${\displaystyle 4}$
${\displaystyle (65536,2^{65536}]}$	${\displaystyle 5}$

Verwendung

Der iterierte Logarithmus spielt eine Rolle bei der Abschätzung der Laufzeit für die Multiplikation großer ganzer Zahlen. Der bisher beste Algorithmus dafür hat eine asymptotische Laufzeit von

${\displaystyle O\left(n\cdot \log(n)\cdot 2^{3\log ^{*}(n)}\right)}$,

siehe auch Schönhage-Strassen-Algorithmus.

Literatur

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Algorithmen – Eine Einführung Oldenburger Wissenschaftsverlag, München 2010, ISBN 978-3-486-59002-9.