Ionosphärischer Wellenleiter

Niederfrequente elektromagnetische Wellen (< 30 kHz) breiten sich im Bereich zwischen Erdoberfläche und der ionosphärischen D-Schicht (< 90 km Höhe) ähnlich wie in einem Mikro-Wellenleiter aus. Die Wellen werden darin so gebündelt, dass sie im Wellenleiter geführt werden. Die strahlenoptische Betrachtungsweise verliert dabei ihre Gültigkeit. Dieser Ausbreitungsbereich wird deshalb ionosphärischer Wellenleiter genannt.

Einführung

Die Radiowellenausbreitung in der Ionosphäre hängt von der Frequenz, vom Einfallswinkel, von der Tages- und Jahreszeit, vom Erdmagnetfeld, und von der Sonnenaktivität ab. Bei vertikalem Einfall können Wellen mit einer Frequenz größer als die Elektronenplasmafrequenz des F-Schicht-Maximums

f_{\text{e}}=9{\sqrt {N_{\text{e}}}}~{\text{kHz}}

(N_e in cm⁻³ ist die Elektronendichte) die Ionosphäre fasst ungestört durchdringen. Wellen mit Frequenzen kleiner f_e werden dagegen in den ionosphärischen D-, E- und F-Schichten reflektiert.[1][2] f_e ist am Tage von der Größenordnung 8–15 MHz, Nachts geringer. Bei schrägem Einfall wird diese kritische Frequenz größer.

Längstwellen (3–30 kHz, very low frequencies, VLF), und extrem lange Wellen (< 3 kHz, extremely low frequencies, ELF) werden bereits an der ionosphärischen E- und D-Schicht reflektiert. Eine Ausnahme bildet die Whistler-Ausbreitung von Blitz-Signalen entlang der geomagnetischen Kraftlinien in die Magnetosphäre.[1][3]

Die Dimensionen der Wellenlängen der VLF-Wellen (10–100 km) sind bereits vergleichbar mit der Höhe der ionosphärischen D-Schicht (etwa 70 km am Tage und 90 km während der Nacht). Daher besitzt die strahlenoptische Betrachtungsweise nur noch beschränkt Gültigkeit, und die wellenoptische Methode wird (zumindest bei größeren Entfernungen) notwendig. Das Gebiet zwischen Erde und ionosphärischer D-Schicht verhält sich also wie ein Wellenleiter gegenüber VLF- und ELF-Wellen.

Elektromagnetische Wellen im ionosphärischen Plasma in Anwesenheit des Erdmagnetfeldes hören auf zu existieren, falls ihre Frequenz kleiner als die Gyrofrequenz der Ionen (etwa 1 Hz) ist. Wellen mit kleineren Frequenzen heißen hydromagnetische Wellen. Die erdmagnetischen Pulsationen mit Perioden von Sekunden bis Minuten sowie die Alfvén-Wellen gehören zu diesem Wellentyp.

Übertragungsfunktion

Der Prototyp einer vertikalen Stabantenne ist ein vertikaler Hertz’scher Dipol, in dem ein elektrischer Wechselstrom der Frequenz $f$ fließt. Seine Ausstrahlung von elektromagnetischen Wellen in den Wellenleiter zwischen Erde und Ionosphäre kann durch eine Übertragungsfunktion $T(\rho ,\omega )$ beschrieben werden:

E_{\text{z}}(\rho ,\omega )=T(\rho ,\omega )E_{\text{o}}(\rho ,\omega )

(1)

wobei $E_{\text{z}}$ die Vertikalkomponente des elektrischen Feldes am Empfänger im Abstand ρ vom Sender, $E_{\text{o}}$ das elektrische Feld des Hertz’schen Dipols im freien Raum und $\omega =2\pi f$ die Kreisfrequenz sind. Im freien Raum ist $T=1$ . Ersichtlich ist der Wellenleiter dispersiv, da die Übertragungsfunktion von der Frequenz abhängt. Das bedeutet, dass Phasen- und Gruppengeschwindigkeit frequenzabhängig sind.

Strahlentheorie

Im VLF-Bereich ist die Übertragungsfunktion die Summe von Bodenwelle sowie von mehrfach an der ionosphärischen D-Schicht reflektierten Strahlen (Abb. 1).

Am Erdboden wird die Bodenwelle (Sommerfeld’sche Bodenwelle) gedämpft. Dieser Energieverlust hängt von der Orographie entlang des Strahlenweges ab.[4] Für VLF-Wellen ist dieser Effekt bei kürzeren Abständen zwischen Sender und Empfänger jedoch relativ gering, so dass in erster Näherung der Reflexionsfaktor des Erdbodens $R_{\text{e}}=1$ ist.

Abbildung 1. Geometrie der Strahlenwege innerhalb der ionosphärischen Wellenleiters. Die Bodenwelle und zwei reflektierte Raumwellen sind dargestellt

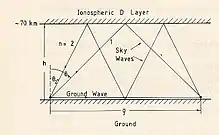
Bei kürzeren Entfernungen sind nur Bodenwelle und die einfach reflektierte Raumwelle von Bedeutung. Die D-Schicht verhält sich für VLF-Wellen in erster Näherung wie ein magnetischer Wall ( $R_{\text{i}}=-1$ ) mit einer scharfen Begrenzung in der Höhe $h$ . Das bedeutet einen Phasensprung von 180° am Reflexionspunkt.[1][4] Tatsächlich wächst die Elektronendichte der D-Schicht mit der Höhe, und der wahre Strahlenweg ist gekrümmt.

Die Summe von Bodenwelle und einfach reflektierter Welle zeigt ein Interferenzminimum dort, wo die Differenz der Strahlenwege eine halbe Wellenlänge (oder eine Phasendifferenz von 180°) beträgt. Das letzte am Erdboden gemessene Interferenzminimum befindet sich in einem Abstand von

\rho _{1}\approx {\frac {2fh^{2}}{c}}

(2)

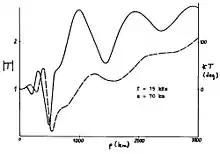
vom Sender (mit c der Lichtgeschwindigkeit). Im Beispiel der Abb. 2 sind dies etwa 500 km.

Abbildung 2. Normalisierte vertikale Feldstärke E_z (Übertragungsfunktion) als Funktion des Abstandes ρ zwischen Sender und Empfänger nach Betrag (volle Linie; linke Ordinate) und Phase (gestrichelte Linie; rechte Ordinate). Der Sender ist ein vertikaler Hertz’scher Diplol der Frequenz von f = 15 kHz. Die virtuelle Reflexionshöhe beträgt 70 km. Dies entspricht Tagesbedingungen in mittleren Breiten. Das Amplitudenminimum in etwa ρ = 500 km Entfernung ist das letzte Interferenzminimum zwischen Boden- und einfach reflektierter Welle in der strahlenoptischen Theorie und das erste Interferenzminimum der wellenoptischen Theorie (Mode-Theorie)

Wellenoptische Theorie

Für VLF-Wellen ist die Strahlentheorie bei größeren Entfernungen zwischen Sender und Empfänger nicht mehr brauchbar, da zu viele mehrfach reflektierte Wellen involviert sind, und die Summe divergiert. Hier kann man die wellenoptische Theorie anwenden. In dieser Theorie ist es auch möglich, die gekrümmte Erde zu berücksichtigen. Die Wellenmoden sind die Eigenmoden im Wellenleiter zwischen Erde und Ionosphäre.[4][5] Diese Wellenmoden besitzen individuelle Vertikalstrukturen ihrer elektrischen Feldstärken im Wellenleiter mit Maximalamplituden am Erdboden und verschwindender Amplitude am oberen Rand (der ionosphärischen D-Schicht). Im Falle des fundamentalen ersten Modes ist dies eine Viertelwellenlänge. Mit wachsender Frequenz werden die Eigenmoden evaneszent. Dies geschieht bei der Grenzfrequenz f_co. Diese ist für den ersten Mode[1]

f_{\text{co}}={\frac {c}{4h}}\approx 1~{\text{kHz}}

Bei kleinerer Frequenz kann sich dieser Mode nicht mehr ausbreiten (Abb. 3).

Die Dämpfung der Moden wächst mit der Wellenzahl $n$ . Daher sind im Wesentlichen nur der erste und der zweite Mode von Bedeutung. Das erste Interferenzminimum beider Moden befindet sich in gleichen Abstand wie in der strahlenoptischen Theorie (Gl. 2), was die Äquivalenz beider Theorien veranschaulicht. Wellen- und strahlenoptische Theorie sind zwei Näherungen der Übertragungsfunktion $T$ in Gl. 1 mit zwei unterschiedlichen Konvergenzbereichen.[6] Aus Abb. 2 wird deutlich, dass der Abstand zwischen den Interferenzminima der beiden Modes gleich ist; im Beispiel der Abb. 2 etwa 1.000 km. Der erste Mode dominiert bei Entfernungen größer als etwa 1500 km, da der zweite Mode stärker als der erste Mode gedämpft wird.

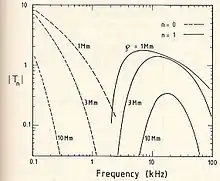
Abbildung 3. Amplitude der Übertragungsfunktion des ersten und des nullten Modes als Funktion der Frequenz bei Abständen von 1.000, 3.000 und 10.000 km am Tag

Im ELF-Bereich ist nur noch die wellenoptische Lösung möglich. Der fundamentale Mode ist der nullte Mode (Abb. 3). Die D-Schicht verhält sich hier in erster Näherung wie ein elektrischer Wall mit dem Reflexionsfaktor $R_{\text{i}}=1$ . Für den Mode Null ist die Vertikalstruktur der elektrischen Feldstärke eine Konstante.

Der Mode Null ist von besonderer Bedeutung für die Schumann-Resonanzen. Ihre Wellenlängen sind der m-te Teil des Erdumfanges. Sie besitzen die Frequenz

f_{\text{m}}={\frac {mc}{2a\pi }}(m=1,2,\ldots )

mit a dem Erdradius. Die ersten Resonanzfrequenzen liegen bei 7,5, 15 und 22,5 Hz. Schumann-Resonanzen werden von Blitzen angeregt, deren spektrale Amplituden in diesem Frequenzbereich verstärkt werden.[4][7]

Eigenschaften des Wellenleiters

Die obige Darstellung des Wellenleiters gibt natürlich nur ein extrem vereinfachtes Bild wider. Für eine detailliertere Betrachtungsweise sind numerische Modelle notwendig. Besonders schwierig ist die Berücksichtigung horizontaler und vertikaler Inhomogenitäten. Auf Grund der endlichen Ausdehnung des Wellenleiters wird die Feldstärke an den Antipodenpunkten verstärkt.[4] Unter dem Einfluss des Erdmagnetfeldes wird der iononosphärische Reflexionsfaktor eine Matrix. Das heißt, dass eine vertikal polarisierte Welle nach der Reflexion an der Ionosphäre sich in eine vertikal polarisierte und eine horizontal polarisierte Welle aufspaltet. Schließlich ist das Erdmagnetfeld dafür verantwortlich, dass bei der Ausbreitung von West nach Ost die Wellen weniger stark gedämpft werden als bei der Ausbreitung von Ost nach West. Eine weitere Nichtreziprozität erfolgt in der Umgebung des tiefen Interferenzminimums der Gl. 2. Während der Zeit von Sonnenaufgang- und Untergang gibt es zeitweilig einen Phasengewinn oder Verlust von 360° wegen des irreversiblen Verhaltens der an der Ionosphäre reflektierten Welle.

Die Dispersionseigenschaft des ionosphärischen Wellenleiters erlaubt die Ortung von Gewitterzellen. Ein Blitz sendet ein breites Spektrum von VLF- und ELF-Wellen aus, Spherics genannt. Die Differenz der Gruppenlaufzeitverzögerungen benachbarter Frequenzen eines solchen Sferics ist direkt proportional dem Abstand ρ zwischen Sender und Empfänger. Zusammen mit einer Richtungsbestimmung des ankommenden Signals bekommt man eine Ortsbestimmung seines Ursprungs von einer einzigen Station aus mit einer Reichweite von mehreren 1000 km (Atmosphärische Störungen)[6][8]. Mit Hilfe der Messung von Schumann-Resonanzen an wenigen Stationen kann die globale Gewitteraktivität ermittelt werden.[9]

Einzelnachweise

K. Davies: Ionospheric Radio. Peregrinus, London 1990.
K. Rawer: Wave Propagation in the Ionosphere. Kluwer Publ., Dordrecht 1993.
Robert A. Helliwell: Whistlers and Related Ionospheric Phenomena. Dover Publications, 2006, ISBN 0-486-44572-0 (Ursprünglich herausgegeben von Stanford University Press, Stanford, California, 1965).
J. R. Wait: Electromagnetic Waves in Stratified Media. McMillan, New York 1979.
K. G. Budden: The Propagation of Radiowaves. Cambridge University Press, Cambridge 1985.
H. Volland: Atmospheric Electrodynamics. Springer, Heidelberg 1984.
A. P. Nickolaenko, M. Hayakawa: Resonances in the Earth–ionosphere cavity. Kluwer Academic Publishers, Dordrecht/ Boston/ London, 2002.
Christoph Grandt: Thunderstorm Monitoring in South Africa and Europe by Means of Very Low Frequency Sferics. In: Journal of Geophysical Research. Band 97, D16, 1992, S. 18215–18226, doi:10.1029/92JD01623.
S. J. Heckman, E. Williams,: Total global lightning inferred from Schumann resonance measurements. In: J. G. R.. 103, Nr. D24, 1998, S. 31775–31779. bibcode:1998JGR...10331775H. doi:10.1029/98JD02648.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Davies-1] K. Davies: Ionospheric Radio. Peregrinus, London 1990.

[2] K. Rawer: Wave Propagation in the Ionosphere. Kluwer Publ., Dordrecht 1993.

[RAH1965-3] Robert A. Helliwell: Whistlers and Related Ionospheric Phenomena. Dover Publications, 2006, ISBN 0-486-44572-0 (Ursprünglich herausgegeben von Stanford University Press, Stanford, California, 1965).

[Wait-4] J. R. Wait: Electromagnetic Waves in Stratified Media. McMillan, New York 1979.

[5] K. G. Budden: The Propagation of Radiowaves. Cambridge University Press, Cambridge 1985.

[Volland-6] H. Volland: Atmospheric Electrodynamics. Springer, Heidelberg 1984.

[Nick_2002-7] A. P. Nickolaenko, M. Hayakawa: Resonances in the Earth–ionosphere cavity. Kluwer Academic Publishers, Dordrecht/ Boston/ London, 2002.

[8] Christoph Grandt: Thunderstorm Monitoring in South Africa and Europe by Means of Very Low Frequency Sferics. In: Journal of Geophysical Research. Band 97, D16, 1992, S. 18215–18226, doi:10.1029/92JD01623.

[Heckman-9] S. J. Heckman, E. Williams,: Total global lightning inferred from Schumann resonance measurements. In: J. G. R.. 103, Nr. D24, 1998, S. 31775–31779. bibcode:1998JGR...10331775H. doi:10.1029/98JD02648.