Huber-k-Schätzer

Der Huber-k-Schätzer ist eine spezielle Schätzfunktion für M-Schätzer (Robuste Schätzverfahren). Er wird verwendet, um den Lageparameter einer normalverteilten Grundgesamtheit zu schätzen. Er wurde 1963 vom Schweizer Mathematiker Peter J. Huber entwickelt.[1]

$\rho (z)$	$\psi (z)$
$\rho (z)_{H}={\begin{cases}{\frac {1}{2}}z^{2}&\|z\|\leq {}k\\k\|z\|-{\frac {1}{2}}k^{2}&\|z\|>k\end{cases}}$	$\psi (z)_{H}={\begin{cases}z&\|z\|\leq {}k\\k\operatorname {sgn} (z)&\|z\|>k\end{cases}}$

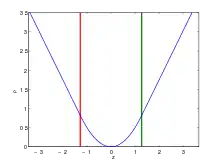
Verlauf der ρ-Funktion des Huber-k-Schätzers für k=1,28

Die Idee dahinter ist, dass große Werte, die als Ausreißer angesehen werden, ab einer bestimmt Größe $k$ keinen quadratischen Einfluss mehr haben sollen.

$k$ ist eine sogenannte Tuning-Konstante. Der gebräuchlichste Wert ist $k=1{,}28$ , was dem 0,9-Quantil der Standardnormalverteilung entspricht.

Literatur

Joachim Hartung, Bärbel Elpelt, Karl-Heinz Klösener: Statistik: Lehr- und Handbuch der angewandten Statistik. Oldenbourg Verlag, München/Wien 2002, S. 869–872

Einzelnachweise

Peter J. Huber: Robust Estimation of a Location Parameter. In: Annals of Mathematical Statistics. 35, Nr. 1, 1964, S. 73–101.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Peter J. Huber: Robust Estimation of a Location Parameter. In: Annals of Mathematical Statistics. 35, Nr. 1, 1964, S. 73–101.