George Odom
George Phillips Odom, Jr (1941 – 18. Dezember 2010[1]) war ein US-amerikanischer Künstler und Amateur-Geometer, der vor allem für seine Beiträge zum Goldenen Schnitt (Φ) bekannt ist.
Leben und Werk
In den 1960ern wurde Odom zunächst in New York für seine aus Glasfasern konstruierten Lichtmaschinen bekannt, die er in der Knoll International Gallery in Manhattan ausstellte. Odom litt unter Depressionen, die später in einem Selbstmordversuch gipfelten und schließlich dazu führten, dass er seit Beginn der 1980er in dem Hudson River Psychiatric Center in Poughkeepsie weitgehend isoliert von der Außenwelt lebte.[2][3]

Odoms Interesse an Geometrie wurde durch den Besuch einer Ausstellung von Buckminster Fuller in den 1960ern geweckt. Mitte der 1970er Jahre schrieb er dann dem kanadischen Geometer Donald Coxeter, da er der Ansicht war, seine künstlerische Arbeit wäre auch unter mathematischen Gesichtspunkten von einem gewissen Interesse. Es entwickelte sich dann eine regelmäßige Korrespondenz mit Coxeter und einem weiteren Mathematiker, dem Benediktiner-Mönch Magnus Wenniger aus Minnesota, die über 25 Jahre andauern sollte. Die beiden Mathematiker wurden damit zu einem der wenigen regelmäßigen Kontakte zur Außenwelt, die Odom noch besaß, seitdem er im Hudson River Psychiatric Center lebte. Er korrespondierte mit ihnen nicht nur über Mathematik, sondern auch über Psychologie, Philosophie, Religion und das Weltgeschehen. In der Mathematik interessierte er sich für geometrische Figuren und den goldenen Schnitt. Er entdeckte mehrere bis dahin noch unbekannte Beispiele für das Auftreten des Goldenen Schnittes in verschiedenen elementaren geometrischen Figuren. Die beiden Mathematiker gaben Odoms Erkenntnisse und Anregungen in ihren Vorlesungen und Gesprächen weiter und Coxeter verarbeitete sie auch in einigen Publikationen. Am bekanntesten ist die Konstruktion des Goldenen Schnittes mithilfe eines gleichseitigen Dreiecks und dessen Umkreises. Coxeter formulierte aus dieser Konstruktion eine Aufgabe, die 1983 als Problem Nr. E3007 im American Mathematical Monthly veröffentlicht wurde:[2][3]
- Seien A und B die Seitenmitten der Seiten EF und ED des gleichseitigen Dreiecks DEF. Verlängere AB so, dass die Verlängerung den Umkreis des Dreiecks DEF in C schneidet. Zeige nun, dass B die Strecke AC im Goldenen Schnitt teilt.[3]

Odom fand noch eine weitere Möglichkeit, den Goldenen Schnitt über ein gleichseitiges Dreieck zu konstruieren:
- Gegeben ist ein gleichseitiges Dreieck ABC mit der Höhe von C auf AB. Sei D der Fußpunkt der Höhe. Nun verlängert man die Höhe über D hinaus um die Länge der Strecke BD. Sei E der Endpunkt der Verlängerung. Nun verbindet man die Punkte E und A und verlängert diese Strecke über A hinaus so, dass sie den Kreis um D mit dem Radius |CD| in F schneidet. Nun teilt A die Strecke EF im Goldenen Schnitt.[3]
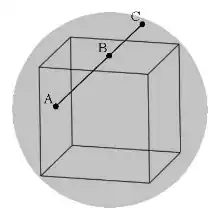
Odom beschäftigte sich mit Modellen und Skulpturen, die aus 3-dimensionalen geometrischen Figuren zusammengesetzt waren, und untersuchte auch dort das Auftreten von Goldenen Schnitten. Dabei entdeckte er zwei einfache Beispiele für dessen Auftreten in platonischen Körpern, nämlich im Tetraeder und im Würfel. Wenn man die Seitenmitten einer Dreiecksfläche eines Tetraeders verbindet und diese Strecke so verlängert, dass sie die Umkugel des Tetraeders schneidet, dann bilden die drei Punkte eine Strecke, die im Goldenen Schnitt geteilt ist. Schneidet man die Umkugel entlang der Ebene, in der die Dreiecksfläche mit den Seitenmitten liegt, auf, so ergibt sich in dieser Ebene die Konfiguration der Aufgabe E3007. Verbindet man bei einem Würfel die Flächenmitten zweier beliebiger benachbarter Oberflächen und verlängert die Strecke so, dass sie die Umkugel des Würfels in einem Punkt schneidet, dann bildet dieser Punkt zusammen mit den beiden Seitenmitten ebenfalls eine Strecke, die im Goldenen Schnitt geteilt wird.[3]
Als Wenniger ihn 2003 von dem Tode Coxeters unterrichtete, sagte Odom: „Ich weiß nicht, was ich ohne dich, Socantens [sein Arzt] und Coxeter gemächt hätte. Ihr drei wart mein einziger Kontakt zur Menschheit.“[3]
2007 wurde Odom von dem Princeton-Mathematiker John Horton Conway in Poughkeepsie besucht.[2]
Literatur
- Siobhan Roberts: Cubic Connection. In: The Walrus, April 2007
- Siobhan Roberts: A Reclusive Artist Meets Minds with a World-Famous Geometer: George Odom and H.S.M. (Donald) Coxeter. Leonardo, Band 40, Nr. 2, 2007, S. 175–177 (JSTOR)
- Doris Schattschneider: Coxeter and the Artists: Two-way Inspiration. In: Harold Scott Macdonald Coxeter (Hrsg.), Chandler Davis (Hrsg.), Erich W. Ellers (Hrsg.): The Coxeter Legacy: Reflections and Projections. AMS, 2006, ISBN 0-8218-3722-2, S. 255–280, hier S. 268–270 (Auszug in der Google-Buchsuche)
Weblinks
- Pat Ballew: The Geometric Beauty of a Troubled Mind
- Golden Ratio in Equilateral Triangle on the Shoulders of George Odom auf cut-the-knot.org
Einzelnachweise
- Siobhan Roberts: Genius At Play: The Curious Mind of John Horton Conway. Bloomsbury Publishing USA, 2015, ISBN 9781620405949, S. 440
- Siobhan Roberts: Cubic Connection. In: The Walrus, April 2007
- Doris Schattschneider: Coxeter and the Artists: Two-way Inspiration. In: Harold Scott Macdonald Coxeter (Hrsg.), Chandler Davis (Hrsg.), Erich W. Ellers (Hrsg.): The Coxeter Legacy: Reflections and Projections. AMS, 2006, ISBN 0-8218-3722-2, S. 255–280, hier S. 268–270 (Auszug in der Google-Buchsuche)