Fraktale Tonkompression
Fraktale Tonkompression ist ein Verfahren zur verlustbehafteten Kompression von digitalisierten, eindimensionalen Signalen, wie z. B. Tonsignalen, bei dem die Selbstähnlichkeit in den Signalen ausgenutzt wird.
Ihren Ursprung fand dieses Verfahren in der fraktalen Bildkompression, die auf die theoretischen Grundlagen von Michael F. Barnsley und Alan D. Sloan zurückgeht.
Prinzip
Die Idee beruht auch hier auf einer bestimmten Sorte von Fraktalen, dem Iterierten Funktionen-System (IFS). Hier werden komplexe Abbildungen mit einer Menge von affinen Abbildungen des Signales in sich selbst erstellt.
Im Gegensatz zu Bildern besitzen Audiosignale keine zweite Dimension, sondern sind eindimensionale Signale. Trotzdem kann man die prinzipielle Funktion der fraktalen Algorithmen aus der Bildkompression problemlos auf diese Art von Signalen übertragen.
Das Kodierverfahren selbst ist von der Vorgehensweise her identisch mit dem der Bildkompression. Der wesentliche Unterschied besteht in der Anzahl der möglichen Transformationen, die auf ein eindimensionales Signal angewandt werden können. Bedingt durch die fehlende zweite Dimension bleiben hier deutlich weniger Möglichkeiten. Konkret sind es sieben relevante Transformationen:
- Identität s(t) → s(t)
- Vertikale Verschiebung (Offset) s(t) → s(t) + o
- Horizontale Verschiebung (Zeit) s(t) → s(t + Δ t)
- Strecken/Stauchen (Dynamik) s(t) → d × s(t)
- Vertikale Spiegelung (Phasendrehung) s(t) → -1 × s(t)
- Horizontale Spiegelung (Zeitinversion) s(t) → s(-t)
- Kontraktion (Zeitdilatation) s(t) → s(a × t)
Die Transformationen 4 und 5 sowie 6 und 7 lassen sich zusammenfassen, sodass effektiv nur fünf mögliche Transformationen zur Verfügung stehen.
Die Kodierung läuft dann nach einem einfachen Schema ab. Der Algorithmus unterteilt das Signal in eine definierte Anzahl von Zielblöcken a und Ursprungsblöcken b und versucht, für jeden einzelnen dieser Zielblöcke eine Transformation zu finden, die einen Ursprungsblock transformiert und damit den Zielblock möglichst ideal abbildet.
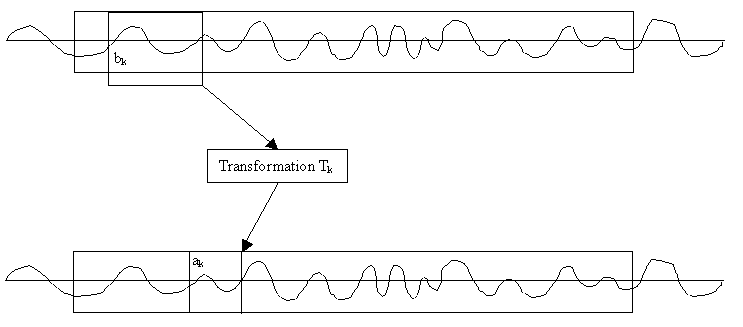
Zu beachten ist, dass der Block größer sein muss als der Block , da fraktale Kompressionen auf kontrahierenden Funktionen beruhen. Wurde für jeden Zielblock eine entsprechende Transformation gefunden, wird das eigentliche Signal verworfen und an seiner Stelle nur die ermittelten Transformationen gespeichert. Der bei diesem Verfahren erreichbare Kompressionsfaktor ist einzig durch die Anzahl der (Abtast-)Werte pro Zielblock bestimmt. Je mehr Werte ein Zielblock enthielt, desto größer ist der Kompressionsfaktor. Theoretisch sind somit beliebig hohe Kompressionsfaktoren erreichbar.
Die Suche nach einem Satz solcher Transformationen ist extrem aufwendig, was neben verschiedenen ungelösten Qualitätsproblemen der Hauptgrund ist, weshalb eine fraktale Kompression von Tonsignalen niemals ernsthaft in Betracht gezogen wurde.
Die Rekonstruktion eines Tonsignals erfolgt iterativ. Es wird mit einem beliebigen Signal begonnen, das in seiner Gesamtlänge dem ursprünglichen Signal entsprechen muss. Dann werden alle gespeicherten Transformationen durchgeführt. Das so erhaltene Signal dient wieder als Ausgangssignal für die nächste Iteration. Mit jeder Iteration wird das rekonstruierte Signal dem ursprünglichen Signal ähnlicher. Diese Iterationen werden so oft durchgeführt, bis keine Verbesserung mehr erreicht wird.
Qualität
Die erzielbare akustische Qualität einer fraktalen Tonkompression hängt zum einen stark vom zu erreichenden Kompressionsfaktor ab, ist zum anderen aber auch von einigen, durch das Verfahren bedingte Besonderheiten, abhängig. Generell gilt: Je höher der Kompressionsfaktor, desto schlechter die Qualität. Durch das Verfahren als solches gibt es zwei wesentliche Probleme, die die Qualität nachhaltig beeinflussen. Fraktale Kompressionen beruhen auf kontrahierenden Funktionen. Das bedeutet, dass immer ein Verlust hochfrequenter Signalanteile stattfindet. Die Ursache dafür liegt im Abtasttheorem und kann nicht umgangen werden. Außerdem kommt es, durch die auf Blöcken basierte Kompression, an den Blockgrenzen im dekodierten Signal zu Phasensprüngen, die sich akustisch als Knistern äußern. Dieses Problem kann durch entsprechende Nachbearbeitung des dekodierten Signals mit z. B. Wavelet-Transformationen gemildert oder sogar beseitigt werden.
Im Allgemeinen erreicht eine fraktale Kompression jedoch nicht die Qualität von z. B. psychoakustischen Verfahren wie MP3 oder RealAudio.
Siehe auch
Literatur
- Michael F. Barnsley, Lyman P. Hurd: Bildkompression mit Fraktalen. Vieweg, Braunschweig u. a. 1996, ISBN 3-528-05464-6.
- Reiko Klimpsch: Entwicklung und Analyse eines fraktalen Verfahrens zur Tonkompression. Diplomarbeit, 2002, .
- Stephan Schneider: Entwicklung und Analyse eines fraktalen Kodierverfahrens für Sprachsignale (= Schriftenreihe Prozeßmodelle. Bd. 4). Köster, Berlin 2001, ISBN 3-89574-416-6 (Zugleich: Cottbus, Technische Universität, Dissertation, 2001).