Euklidische Relation

Eine euklidische Relation ist in der Mathematik eine binäre Relation, für die Euklids Axiom „Was demselben gleich ist, ist auch einander gleich“[1] gilt.

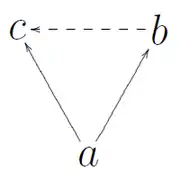
Für eine rechts-euklidische Relation gilt: vorausgesetzt, dass a zu b und a zu c in gleicher Beziehung steht (durchgehende Pfeile), so stets auch b zu c (gestrichelter Pfeil)

Definition

Eine binäre Relation R auf einer Menge X heißt euklidisch (oder auch rechts-euklidisch), wenn für beliebige Elemente a, b, c in X die folgende Bedingung erfüllt ist: steht a zu b und a zu c in gleicher Beziehung, so steht auch b zu c in dieser Beziehung.[2] Dies lässt sich auch prädikatenlogisch ausdrücken mit $\forall a,b,c\in X(aRb\land aRc\implies bRc)$ .

Dual dazu heißt eine Relation R auf X links-euklidisch, wenn für beliebige a, b, c in X gilt: stehen sowohl b als auch c in Beziehung zu a, dann steht auch b in Beziehung zu c, formal $\forall a,b,c\in X(bRa\land cRa\implies bRc)$ .

Eigenschaften

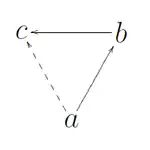
Für Transitivität gilt: vorausgesetzt, dass a zu b und b zu c in der Relation steht, so stets auch a zu c

Die Eigenschaft euklidisch zu sein unterscheidet sich von der Transitivität. Zum Beispiel ist die Relation ≤ auf den natürlichen Zahlen transitiv, doch nicht rechts-euklidisch,[3] während die durch $xRy:\Leftrightarrow 0\leq x\leq y+1\leq 2$ definierte Relation $R$ auf den natürlichen Zahlen nicht transitiv,[4] jedoch rechts-euklidisch ist.

Für eine symmetrische Relation sind die Eigenschaften Transitivität, rechts- und links-euklidisch koinzident. Doch kann auch eine nicht-symmetrische Relation sowohl transitiv als auch rechts-euklidisch sein, z. B. xRy definiert durch y=0.

Eine Relation, die sowohl rechts-euklidisch als auch reflexiv ist, ist notwendig auch symmetrisch und damit eine Äquivalenzrelation.[2][5] Ebenso ist jede links-euklidische und reflexive Relation notwendig eine Äquivalenz.

Der Bildbereich einer rechts-euklidischen Relation ist stets eine Teilmenge[6] ihres Urbildbereichs. Die Einschränkung einer rechts-euklidischen Relation auf ihren Bildbereich ist stets reflexiv[7] und somit eine Äquivalenzrelation. Ebenso ist der Urbildbereich einer links-euklidischen Relation stets eine Teilmenge ihres Bildbereichs, und die Beschränkung einer links-euklidischen Relation auf ihren Urbildbereich eine Äquivalenz.

Eine Relation R ist links- und rechts-euklidisch genau dann, wenn ihr Urbild- und ihr Bildbereich übereinstimmen und R auf dieser Menge eine Äquivalenzrelation ist.[8]

Eine rechts-euklidische Relation ist stets quasitransitiv,[9] ebenso eine links-euklidische Relation.[10]

Eine konnexe rechts-euklidische Relation ist stets auch transitiv,[11] ebenso eine konnexe links-euklidische Relation.[10]

Wenn X mindestens 3 Elemente hat, kann eine konnexe rechts-euklidische Relation R auf X nicht antisymmetrisch sein,[12] gleiches gilt für eine konnexe links-euklidische Relation auf X.[10] Auf der zweielementigen Menge X = { 0, 1 } ist z. B. die durch $xRy:\Leftrightarrow y=1$ definierte Relation konnex, rechts-euklidisch und antisymmetrisch; $xRy:\Leftrightarrow x=1$ ist auf dieser Menge konnex, links-euklidisch und antisymmetrisch.

Einzelnachweise und Anmerkungen

Das Buch I der Elemente von Euklid enthält einleitend eine axiomatische Grundlegung, in der dieser Grundsatz als 1. Axiom allgemeiner Regeln der Gleichheit aufgeführt ist („Τὰ τῷ αὐτῷ ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα“); siehe hierzu W.-D. Geyer: Euklid: Die Elemente – eine Übersicht. Vorlesung über antike Mathematik, SS 2001, S. 3 (PDF; 275 kB).
Ronald Fagin: Reasoning About Knowledge. MIT Press, 2003, ISBN 978-0-262-56200-3, S. 60 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).
Da z. B. 0≤2 und 0≤1 gilt, aber nicht 2≤1.
Da z. B. 2R1 und 1R0 gilt, aber nicht 2R0.
Denn aus xRy und xRx folgt yRx.
Gleichheit von Urbild- und Bildbereich ist nicht notwendig: die Relation xRy definiert durch y=min{x,2} ist rechts-euklidisch auf den natürlichen Zahlen und ihr Bildbereich {0,1,2} ist eine echte Teilmenge ihres Urbildbereichs ℕ.
Wenn y im Bildbereich von R liegt, dann folgt aus xRy ∧ xRy für geeignetes x, dass yRy. Dies zeigt auch, dass y im Urbildbereich von R liegt.
Die " $\Rightarrow$ "-Richtung folgt aus dem vorherigen Absatz. — Für die " $\Leftarrow$ "-Richtung nimm an, dass aRb und aRc gelten, dann liegen a,b,c im Urbild- und im Bildbereich von R; also folgt bRc wegen Symmetrie und Transitivität. Die links-euklidische Eigenschaft von R folgt analog.
Wenn xRy ∧ ¬yRx ∧ yRz ∧ ¬zRy gilt, dann liegen sowohl y als auch z im Bildbereich von R. Da R auf dieser Menge eine Äquivalenz ist, folgt aus yRz schon der Widerspruch zRy.
Mit einem analogen Argument, das die Lage von x und y im Urbildbereich von R verwendet.
Wenn xRy ∧ yRz gilt, dann liegen y und z im Bildbereich von R. Da R konnex ist, gilt xRz oder zRx oder x=z.
Da R konnex ist, liegen in ihrem Bildbereich mindestens zwei verschiedene Elemente x und y, für die gilt xRy ∨ yRx. Es gilt sogar xRy ∧ yRx. Dies widerspricht der Antisymmetrie.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Das Buch I der Elemente von Euklid enthält einleitend eine axiomatische Grundlegung, in der dieser Grundsatz als 1. Axiom allgemeiner Regeln der Gleichheit aufgeführt ist („Τὰ τῷ αὐτῷ ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα“); siehe hierzu W.-D. Geyer: Euklid: Die Elemente – eine Übersicht. Vorlesung über antike Mathematik, SS 2001, S. 3 (PDF; 275 kB).

[fagin-2] Ronald Fagin: Reasoning About Knowledge. MIT Press, 2003, ISBN 978-0-262-56200-3, S. 60 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).

[3] Da z. B. 0≤2 und 0≤1 gilt, aber nicht 2≤1.

[4] Da z. B. 2R1 und 1R0 gilt, aber nicht 2R0.

[5] Denn aus xRy und xRx folgt yRx.

[6] Gleichheit von Urbild- und Bildbereich ist nicht notwendig: die Relation xRy definiert durch y=min{x,2} ist rechts-euklidisch auf den natürlichen Zahlen und ihr Bildbereich {0,1,2} ist eine echte Teilmenge ihres Urbildbereichs ℕ.

[7] Wenn y im Bildbereich von R liegt, dann folgt aus xRy ∧ xRy für geeignetes x, dass yRy. Dies zeigt auch, dass y im Urbildbereich von R liegt.

[8] Die " $\Rightarrow$ "-Richtung folgt aus dem vorherigen Absatz. — Für die " $\Leftarrow$ "-Richtung nimm an, dass aRb und aRc gelten, dann liegen a,b,c im Urbild- und im Bildbereich von R; also folgt bRc wegen Symmetrie und Transitivität. Die links-euklidische Eigenschaft von R folgt analog.

[9] Wenn xRy ∧ ¬yRx ∧ yRz ∧ ¬zRy gilt, dann liegen sowohl y als auch z im Bildbereich von R. Da R auf dieser Menge eine Äquivalenz ist, folgt aus yRz schon der Widerspruch zRy.

[analog_Urbild-10] Mit einem analogen Argument, das die Lage von x und y im Urbildbereich von R verwendet.

[11] Wenn xRy ∧ yRz gilt, dann liegen y und z im Bildbereich von R. Da R konnex ist, gilt xRz oder zRx oder x=z.

[12] Da R konnex ist, liegen in ihrem Bildbereich mindestens zwei verschiedene Elemente x und y, für die gilt xRy ∨ yRx. Es gilt sogar xRy ∧ yRx. Dies widerspricht der Antisymmetrie.