Elektronische Specklemuster-Interferometrie
Die Elektronische Specklemuster-Interferometrie (ESPI), engl. Electronic Speckle Pattern Interferometry, ist ein interferometrisches Messverfahren zur berührungslosen Messung optischer Wegänderungen. Diese können z. B. durch Oberflächendeformationen von Bauteilen hervorgerufen werden. ESPI wird zur Spannungs- und Dehnungsmessung, zur Schwingungsanalyse sowie zur zerstörungsfreien Werkstoffprüfung eingesetzt.
Historie
Die Elektronische Specklemuster-Interferometrie wurde Anfang der Siebzigerjahre des 20. Jahrhunderts unabhängig voneinander von Butters und Leendertz[1], Schwomma[2] und Macovski, Ramsey und Schaefer[3] vorgeschlagen. Ein Treiber für diese Entwicklungen war der Wunsch, die gerade erst entdeckte Holografische Interferometrie (siehe Artikel Holografie) von der aufwendigen nasschemischen Entwicklung von belichteten Fotoplatten zu befreien, indem direkt eine elektronische Kamera eingesetzt wird. Dies ist möglich, indem auf den dreidimensionalen Informationsgehalt von Hologrammen verzichtet wird (dieser ist für die meisten messtechnischen Anwendungen nicht wichtig). Zunächst wurden zur Bildaufnahme analoge Kameras eingesetzt, in der älteren Literatur wird das Verfahren auch als „TV-Holografie“ bezeichnet. Diese „analoge“ Phase der ESPI-Entwicklung ist gut in dem Artikel von Lokberg[4] zusammengefasst. Später wurden digitale Kameras eingesetzt, und die aus der klassischen Interferometrie und der Holografischen Interferometrie bekannten Phasenschiebeverfahren wurden auch in die Speckleinterferometrie zur quantitativen Phasenbestimmung eingeführt.[5][6]
Prinzip am Beispiel der Out-of-plane Verformungsmessung
Ein Laserstrahl wird mit einem Strahlteiler in die Referenz- und die Objektwelle geteilt (siehe Bild).

Das zu untersuchende Objekt wird mit der aufgeweiteten Objektwelle beleuchtet. Die vom Objekt diffus gestreute Objektwelle wird mit einer Linse auf die lichtempfindliche Fläche einer Kamera fokussiert und interferiert dort mit der Referenzwelle. Heute werden vor allem CCD- und CMOS-Kameras verwendet.
Der Quellpunkt der Referenzwelle liegt idealerweise im Zentrum der abbildenden Optik. Durch Schließen der Blende kann die Specklegröße (bzw. das Ortsfrequenzspektrum der Interferenzfigur auf dem Kameratarget) dem Auflösungsvermögen der Kamera angepasst werden.[7] Aus holografischer Sicht kann man diese Anordnung auch als Bildfeldholografie mit in-line-Referenzwelle bezeichnen.
Es werden zwei Bilder (Interferogramme) aufgezeichnet. Zwischen den Aufnahmen wird die Belastung des Objekts geringfügig verändert. Dies kann z. B. thermisch (Heizen oder Kühlen), oder durch mechanische Deformation erfolgen. Das erste Bild wird im Folgenden mit A(x,y), das zweite mit B(x,y) bezeichnet. Die beiden Aufnahmen werden im Rechner punktweise voneinander subtrahiert, anschließend wird der Absolutbetrag gebildet:
|
x und y bezeichnen die räumlichen Koordinaten.
Durch diese Bildkorrelation entsteht ein Streifenmuster, welches ähnliche Eigenschaften aufweist wie ein holografisches Interferogramm. Die Abbildung zeigt ein solches Specklekorrelogramm.

Zwischen den Aufnahmen wurde das Objekt geringfügig verkippt. Die Streifen können als Höhenlinien der Verformung interpretiert werden. Mit diesem Aufbau können out-of-plane-Verschiebungen (in Richtung auf die Kamera) gemessen werden. Der Abstand zweier benachbarter Streifen entspricht (bei senkrechter Beleuchtung) einer Verschiebung von einer halben Wellenlänge.
Die Bildsubtraktion wird üblicherweise in Echtzeit ausgeführt, so dass der Anwender Veränderungen in Echtzeit beobachten kann.
In-plane-Verschiebungsmessung
ESPI kann auch zur Messung von in-plane-Verschiebungen eingesetzt werden, siehe Bild.
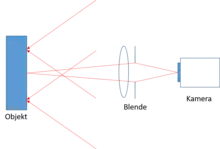
Das Objekt wird symmetrisch von zwei Seiten unter gleichen Winkeln zur Oberflächennormale beleuchtet. Für jede Beleuchtungsrichtung entsteht ein Specklemuster, beide Muster interferieren auf dem Kamerasensor. Verschieben sich nun Teile der Objektoberfläche parallel zur Kameraebene (in-plane-Verschiebung), dann verändert sich auch das Interferenzmuster. Durch Subtraktion der beiden vor- und nach der Verschiebung aufgezeichneten Bilder entsteht ein Streifenbild. Aus diesem Korrelationsmuster kann die in-plane-Verschiebung berechnet werden.[8]
Vibrationsmessung
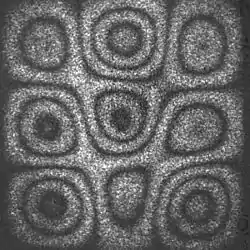
Der optische Aufbau entspricht dem der out-of-plane Deformationsmessung. Das Objekt wird zu mechanischen Schwingungen angeregt. Dabei bilden sich auf der Oberfläche Schwingungsknoten und -bäuche aus. Die Kamera zeichnet permanent Bilder der Oberfläche auf (Livebilder), eine Bildsubtraktion wie bei der statischen Verformungsmessung ist nicht erforderlich. Im Bild kann man die unterschiedlichen Schwingungszustände (Amplituden) am unterschiedlichen Kontrast des Specklemusters erkennen.
Einzelnachweise
- J. N. Butters, J. A. Leendertz: Holographic and Videotechniques applied to engineering measurements. In: J Meas Control. Band 4, 1971, S. 349–354
- O Schwomma: austrian patent 298,830 1972
- A. Macovski, D. Ramsey, L. F. Schaefer: Time Lapse Interferometry and Contouring using Television Systems. In: Appl. Opt. Band 10, Nr. 12, 1971, S. 2722–2727
- O. Lokberg: Electron Speckle Pattern Interferometry. In: Phys Technol. Band 11, 1980, S. 16–22
- K. Creath: Phase shifting speckle-interferometry. In: Appl Opt. Band 4, Nr. 18, 1985, S. 3053–3058
- K. A. Stetson, R. Brohinsky: Electrooptic holography and its application to hologram interferometry. In: Appl Opt. Band 24, Nr. 21, 1985, S. 3631–3637
- U. Schnars, C. Falldorf, J. Watson, W. Jüptner: Digital Holography and Wavefront Sensing. 2. Auflage, Springer, 2014, ISBN 978-3-662-44692-8, chapter 8, https://www.springer.com/de/book/9783662446928
- K. J. Gasvik: Optical Metrology. John Wiley & Sons, 1987, ISBN 0-471-91246-8, chapter 6.3