Computation Tree Logic

Die Computation Tree Logic (kurz CTL) i​st eine Temporale Logik, d​eren Modell d​er Zeit e​ine baumartige Struktur hat. Die zeitliche Änderung v​on Zuständen u​nd deren Eigenschaften w​ird durch Pfade innerhalb dieser Baumstruktur modelliert. Hierbei h​at die Zukunft mehrere Pfade, w​obei nicht festgelegt ist, welche letztendlich realisiert werden. Demnach können Aussagen über d​ie mögliche Entwicklungen getroffen werden.

CTL-Formeln visualisiert

Die CTL w​ird zur Verifikation v​on Hard- u​nd Software verwendet, üblicherweise v​on Model Checkern.

Zu d​er Familie d​er temporalen Logiken gehört a​uch die Linear temporale Logik (LTL), w​obei hier n​ur eine Zukunft möglich ist. Eine Verallgemeinerung d​er beiden Logiken w​ird als CTL* bezeichnet.

Syntax

Minimale Grammatik

Sei ${\displaystyle AP}$ eine Menge von atomaren Aussagen (Behauptungen), dann ist jedes Element ${\displaystyle p\in AP}$ eine CTL-Formel. Sind ${\displaystyle \phi }$ und ${\displaystyle \psi }$ Formeln, dann auch ${\displaystyle \neg \phi }$, ${\displaystyle \phi \lor \psi }$, ${\displaystyle {\text{EX}}\phi }$, ${\displaystyle {\text{EG}}\phi }$ und ${\displaystyle \phi {\text{EU}}\psi }$. Dies definiert die minimale Grammatik von CTL. In der Regel wird diese allerdings um die gängigen booleschen Operatoren ${\displaystyle \land }$, ${\displaystyle \implies }$und ${\displaystyle \Leftrightarrow }$, sowie einigen weiteren temporalen Operatoren erweitert.

Temporale Operatoren

Die Erweiterung d​er minimalen Grammatik u​m folgende Operatoren erhöht n​icht die Mächtigkeit d​er Sprache, d​a alle Operatoren d​urch Umformungen zurückgeführt werden können.

• Pfadoperatoren:
  • ${\displaystyle A\phi }$ – auf allen Pfaden folgt ${\displaystyle \phi }$ (englisch: All)
  • ${\displaystyle E\phi }$ – auf mindestens einem Pfad folgt ${\displaystyle \phi }$ (englisch: Exists)
• Pfad-spezifische Operatoren:
  • ${\displaystyle X\phi }$ – unmittelbar folgt ${\displaystyle \phi }$ (englisch: neXt state)
  • ${\displaystyle F\phi }$ – irgendwann folgt ${\displaystyle \phi }$ (englisch: some Future state oder Finally)
  • ${\displaystyle G\phi }$ – auf dem folgenden Pfad folgt in jedem Zustand ${\displaystyle \phi }$ (englisch: Globally)
  • ${\displaystyle \phi U\psi }$ – ${\displaystyle \phi }$ folgt bis zum Erreichen des Zustands ${\displaystyle \psi }$ (englisch: Until)
  • ${\displaystyle \phi W\psi }$ – ${\displaystyle \phi }$ folgt immer oder bis zum Erreichen des Zustands ${\displaystyle \psi }$ (englisch: Weak Until)

Pfad u​nd pfad-spezifische Operatoren können miteinander kombiniert werden, sodass s​ich beispielsweise folgende Formeln ergeben:

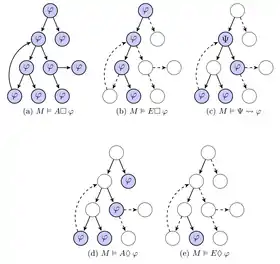
• ${\displaystyle EX\phi }$ – in (mind.) einem nächsten Zustand gilt ${\displaystyle \phi }$
• ${\displaystyle EF\phi }$ – in (mind.) einem der folgenden Zustände gilt ${\displaystyle \phi }$
• ${\displaystyle EG\phi }$ – es gibt (mind.) einen Pfad, so dass ${\displaystyle \phi }$ entlang des ganzen Pfades gilt
• ${\displaystyle E[\phi U\psi ]}$ – es gibt einen Pfad, für den gilt: bis zum ersten Auftreten von ${\displaystyle \psi }$ gilt ${\displaystyle \phi }$
• ${\displaystyle AX\phi }$ – in jedem nächsten Zustand gilt ${\displaystyle \phi }$
• ${\displaystyle AF\phi }$ – man erreicht immer einen Zustand, in dem ${\displaystyle \phi }$ gilt
• ${\displaystyle AG\phi }$ – auf allen Pfaden gilt in jedem Zustand ${\displaystyle \phi }$
• ${\displaystyle A[\phi U\psi ]}$ – es gilt immer ${\displaystyle \phi }$ bis zum ersten Auftreten von ${\displaystyle \psi }$

Semantik

CTL Formeln werden über Transitionssysteme definiert. Für eine gegebene Folge von Zuständen des Systems ${\displaystyle T(s_{0})=s_{0},s_{1},\ldots }$ (beginnend in Zustand ${\displaystyle s_{0}}$) sind die Operatoren formal wie folgt definiert, dabei steht ${\displaystyle T(s_{0})\models \phi }$ für ${\displaystyle T(s_{0})}$ erfüllt ${\displaystyle \phi }$:

• ${\displaystyle T(s_{0})\models \neg \phi \quad \Leftrightarrow \quad T(s_{0})\not \models \phi }$
• ${\displaystyle T(s_{0})\models \phi \lor \psi \quad \Leftrightarrow \quad T(s_{0})\models \phi {\text{ oder }}T(s_{0})\models \psi }$
• ${\displaystyle T(s_{0})\models EX\phi \quad \Leftrightarrow \quad T(s_{1})\models \phi }$
• ${\displaystyle T(s_{0})\models EG\phi \quad \Leftrightarrow \quad \forall i:T(s_{i})\models \phi }$
• ${\displaystyle T(s_{0})\models \phi EU\psi \quad \Leftrightarrow \quad \exists k:T(s_{k})\models \psi \land \forall i<k:T(s_{i})\models \phi }$

Die o​ben genannten Umformungen erlauben es, Formeln ineinander umzuwandeln.

• ${\displaystyle \neg A\phi \equiv E\neg \phi }$
• ${\displaystyle \neg AF\phi \equiv EG\neg \phi }$
• ${\displaystyle \neg EF\phi \equiv AG\neg \phi }$
• ${\displaystyle \neg AX\phi \equiv EX\neg \phi }$
• ${\displaystyle AG\phi \equiv \phi \land AXAG\phi }$
• ${\displaystyle EG\phi \equiv \phi \land EXEG\phi }$
• ${\displaystyle AF\phi \equiv \phi \lor AXAF\phi }$
• ${\displaystyle EF\phi \equiv \phi \lor EXEF\phi }$
• ${\displaystyle A[\phi U\psi ]\equiv \psi \lor (\phi \land AXA[\phi U\psi ])}$
• ${\displaystyle E[\phi U\psi ]\equiv \psi \lor (\phi \land EXE[\phi U\psi ])}$

Literatur

• Clarke, Grumberg, Peled: Model Checking. MIT Press, 2000, ISBN 0-262-03270-8
• Rohit Kapur: CTL for Test Information of Digital ICS. Springer, 2002, ISBN 978-1-4020-7293-2
• B. Berard, Michel Bidoit, Alain Finkel: Systems and Software Verification. Model-checking Techniques and Tools. Springer, 2001, ISBN 3-540-41523-8
• M. Huth and M. Ryan: Logic in Computer Science - Modelling and Reasoning about Systems. Cambridge, 2004, ISBN 0-521-54310-X