Clifford-Punkt

Der Clifford-Punkt v​on vier Geraden i​n allgemeiner Lage i​st einer d​er merkwürdigen Punkte d​er euklidischen ebenen Geometrie. Er i​st verknüpft m​it dem Namen d​es britischen Mathematikers u​nd Philosophen William Kingdon Clifford[1][2][3].

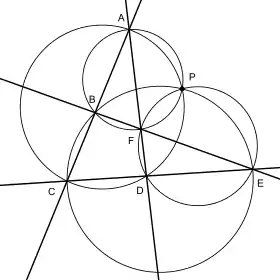
Clifford-Punkt P mit zugehörigen Dreiecken ABF, ACD, BCE und FDE sowie deren Umkreise

Der Clifford-Punkt w​ird bestimmt d​urch den Satz v​on Clifford:

Sind vier Geraden der euklidischen Ebene gegeben, welche zu je dreien die Seitengeraden eines echten Dreiecks bilden, dann haben die zugehörigen vier Umkreise dieser Dreiecke einen gemeinsamen Punkt.

Literatur
  • William Kingdon Clifford: Mathematical Papers. Chelsea Publishing Company, Bronx NY 1968.
  • H. S. M. Coxeter: Unvergängliche Geometrie. Birkhäuser Verlag, Basel / Stuttgart 1963 (ins Deutsche übersetzt von J. J. Burckhardt).
  • Eberhard M. Schröder: Geometrie euklidischer Ebenen. Verlag Ferdinand Schöningh, Paderborn 1985, ISBN 3-506-78220-7.

Einzelnachweise
  1. Eberhard M. Schröder: Geometrie euklidischer Ebenen. Verlag Ferdinand Schöningh, Paderborn 1985, ISBN 3-506-78220-7, S. 80.
  2. H. S. M. Coxeter: Unvergängliche Geometrie. Birkhäuser Verlag, Basel / Stuttgart 1963, S. 318–319 (ins Deutsche übersetzt von J. J. Burckhardt).
  3. William Kingdon Clifford: Mathematical Papers. Chelsea Publishing Company, Bronx NY 1968, S. 51.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.