B*-Baum

Der B*-Baum ist eine Daten- bzw. Indexstruktur in der Informatik und eine Variante des B-Baums, die 1973 von Donald Knuth vorgeschlagen wurde und sich vom B-Baum in der Forderung unterscheidet, dass Knoten mindestens zu 2/3 gefüllt sein müssen (anstatt nur 1/2 gefüllt).[1][2] Dies wird vor allem durch eine veränderte Split-Strategie erreicht, bei der 2 volle Knoten auf 3 Knoten mit einem Füllgrad von 2/3 aufgeteilt werden.

Der Name wird aus historischen Gründen oftmals für den B+-Baum verwendet, eine andere B-Baum-Variante, bei der Daten nur in den Blattknoten gespeichert und durch die Verkettung der Blattknoten Bereichsanfragen effizienter unterstützt werden.

Definition

Knuth definiert einen B*-Baum[1] der Ordnung $m$ durch folgende Forderungen:

Alle Knoten außer die Wurzel haben maximal $m$ Kinder,
alle Knoten außer Wurzel und Blätter haben mindestens ${\frac {2m-1}{3}}$ Kinder,
die Wurzel hat mindestens $2$ und maximal $2\left\lfloor {\frac {2m-2}{3}}\right\rfloor +1$ Kinder,
alle Blätter haben die gleiche Entfernung von der Wurzel und
alle Knoten, die keine Blätter sind, mit $k$ Kindern enthalten $k-1$ Schlüssel.

Unterschiede zum B-Baum

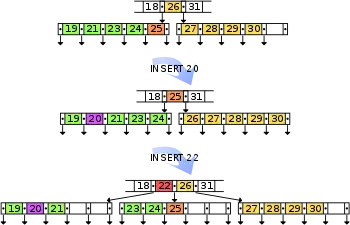
Überlaufbehandlung in einem B*-Baum der Ordnung 6: Beim ersten Insert läuft der Knoten in den Nachbarknoten über, beim zweiten Insert laufen beide Knoten über und ein neuer Knoten wird angelegt.

Genauso wie im B-Baum enthalten auch im B*-Baum die inneren Knoten Daten.[1] Der Hauptunterschied zu B-Bäumen liegt in der zweiten Forderung, dass Knoten zu $2/3$ gefüllt sein müssen. Dazu ist eine Anpassung des B-Baum-Algorithmus zur Überlaufbehandlung nötig. Anstatt bei einem Überlauf sofort einen neuen Knoten anzulegen, wird zuerst überprüft, ob im rechten Nachbarknoten noch Platz ist. Ist dies der Fall, werden die Schlüssel der beiden Knoten und der trennende Schlüssel im Elternknoten gleichmäßig auf die beiden Knoten verteilt. Enthält der zweite Knoten $j$ Schlüssel, so ist der Schlüssel $\lfloor (m+j)/2\rfloor +1$ der neue trennende Schlüssel. Ist im Nachbarknoten ebenfalls kein Platz, wird ein neuer Knoten angelegt und die Schlüssel der beiden ursprünglichen Knoten, der eingefügte Knoten, sowie der trennende Schlüssel des Elternknoten werden auf alle drei Knoten verteilt. Dabei sind die Schlüssel $\lfloor (2m-2)/3\rfloor +1$ und $\lfloor (4m-1)/3\rfloor$ die trennenden Schlüssel im Elternknoten.

Die höhere Datendichte hat einen höheren Verzweigungsgrad und somit eine geringere Baumhöhe zur Folge. Dadurch steigert sich die Performance gegenüber dem B-Baum, da weniger Knoten geladen werden müssen. Für das Level eines Schlüssels und damit die für einen Zugriff nötigen Knoten $l$ gilt in einem B*-Baum der Ordnung $m$ mit $N$ Schlüsseln: $l\leq 1+\log _{\lceil (2m-1)/3\rceil }{\frac {N+1}{2}}$ . Im B-Baum hingegen müssen $l\leq 1+\log _{\lceil m/2\rceil }{\frac {N+1}{2}}$ Knoten für einen Zugriff geladen werden.[1]

Anwendung

Der B*-Baum ist, wie schon der B-Baum, auf die Ablage im Sekundärspeicher optimiert. Zwischen dem Hauptspeicher und dem Sekundärspeicher werden Datenblöcke, auch Seiten (engl. Pages) genannt, fester Größe übertragen. Da Zugriffe auf den Sekundärspeicher gegenüber Berechnungen und Zugriffen auf den Hauptspeicher sehr lange dauern, muss die Zahl der für eine Operation nötigen Seiten aus dem Sekundärspeicher minimiert werden. Die Größe der Knoten wird deshalb so gewählt, dass diese genau in eine Seite passen. Dadurch eignen sich die verschiedenen Varianten des B-Baums sehr gut für Datenbanken und Dateisysteme.

Benennung

Als B*-Baum wird häufig auch eine weitere Variante des B-Baums bezeichnet, die ebenfalls von Knuth beschrieben, aber nicht explizit benannt wird. Diese bekommt von Hartmut Wedekind 1974 ebenfalls den Namen B*-Baum, wird aber 1979 von Douglas Comer zur besseren Abgrenzung als B⁺-Baum bezeichnet.[3][4][2] Allerdings verwendete Rudolf Bayer schon 1977 den Begriff B*-Baum für die später als B⁺-Baum bezeichnete Variante, so dass sich eine eindeutige Abgrenzung nicht mehr vollständig durchsetzen konnte.[5] Vom National Institute of Standards and Technology werden die Varianten des B-Baums nach Comers Unterteilung geführt.[6][7]

Einzelnachweise

Knuth, D. E.: The Art of Computer Programming, Volume III: Sorting and Searching Addison-Wesley, 1973, Seite 476–479
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, Cambridge MA 2001, ISBN 0-262-03293-7.
Comer, D.: Ubiquitous B-Tree ACM Computing Surveys 11, 1979, 2, 121–137
Wedekind, H. On the Selection of Access Paths in a Data Base System IFIP Working Conference Data Base Management, 1974, 385-397
Bayer, R. & Unterauer, K.: Prefix B-Trees ACM Trans. Database Syst., 1977, 2, 11–26
Paul E. Black: "B*-tree", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. U.S. National Institute of Standards and Technology. 6. November 2007, abgerufen am 24. Januar 2011. Available from: https://xlinux.nist.gov/dads/HTML/bstartree.html
Paul E. Black: "B⁺-tree", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 6. November 2007, abgerufen am 24. Januar 2011. Available from: https://xlinux.nist.gov/dads/HTML/bplustree.html

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Knuth1973-1] Knuth, D. E.: The Art of Computer Programming, Volume III: Sorting and Searching Addison-Wesley, 1973, Seite 476–479

[Cormen2001-2] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, Cambridge MA 2001, ISBN 0-262-03293-7.

[Comer1979-3] Comer, D.: Ubiquitous B-Tree ACM Computing Surveys 11, 1979, 2, 121–137

[Wedekind1974-4] Wedekind, H. On the Selection of Access Paths in a Data Base System IFIP Working Conference Data Base Management, 1974, 385-397

[Bayer1977-5] Bayer, R. & Unterauer, K.: Prefix B-Trees ACM Trans. Database Syst., 1977, 2, 11–26

[Nistbstartree-6] Paul E. Black: "B*-tree", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. U.S. National Institute of Standards and Technology. 6. November 2007, abgerufen am 24. Januar 2011. Available from: https://xlinux.nist.gov/dads/HTML/bstartree.html

[Nistbplustree-7] Paul E. Black: "B⁺-tree", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 6. November 2007, abgerufen am 24. Januar 2011. Available from: https://xlinux.nist.gov/dads/HTML/bplustree.html