Acuña-Romo-Gleichung
In der geometrischen Optik und der optischen Technik beschreibt die Acuña-Romo-Gleichung die Lösung des Problems des Entwurfs einer Linse ohne sphärische Aberration.
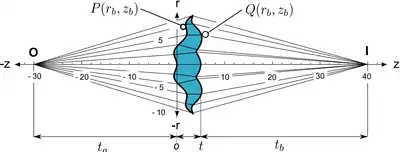
Linse von Acuña-Romo
Prinzip
Die Gleichung gibt an, wie die zweite Oberfläche einer Linse so beschaffen sein soll, dass die durch die erste Brechungsfläche der Linse erzeugte sphärische Aberration für ein Punktobjekt auf der optischen Achse vollständig korrigiert wird.[1]
Ursprung des sphärischen aberrationsfreien Linsendesigns
Einige der wichtigsten Ereignisse für die Konzeption der Linse ohne sphärische Aberration sind:
- Diocles, in seinem Buch "Mirrors ustorios", nachdem festgestellt wurde, dass der Parabolspiegel die Strahlen, die sich in Richtung einer Achse bewegen, in einem einzigen Punkt fokussieren könnte, ist es möglich, eine Linse mit der gleichen Eigenschaft zu erwähnen.[2]
- Ibn Sahl beschäftigt sich mit den optischen Eigenschaften von Spiegeln und gebogenen Linsen. Er wurde als Entdecker des Brechungsgesetzes (Snells Gesetz) beschrieben.[3]
- Rene Descartes untersucht kartesische Ovale und ihre Anwendungen in der Optik.
- Christiaan Huygens schlägt vor, die sphärische Aberration mit einem Satz sphärischer Linsen zu beseitigen. Auch im Vorwort der Arbeit erwähnt "Traité de la lumière", dass Isaac Newton und Gottfried Wilhelm Leibniz das Problem angesprochen haben.[4][5]
- Levi-Civita skizziert die numerische Lösung für das Design von korrigierenden refraktiven Oberflächen.[6]
- G. D. Wasserman und E. Wolf schlagen eine aplanatische Linse vor, die auf einem Integral basiert, das sie mit numerischen Methoden lösen.[7]
- Daniel Malacara Hernández präsentiert ein ungefähres Design einer Linse ohne sphärische Aberration mit zwei asphärischen Oberflächen.[8]
- Psang Dain Lin und Chung-Yu Tsai erhalten das Objektivdesign ohne sphärische Aberration aus der numerischen Lösung eines Systems nichtlinearer Gleichungen.[9]
- Juan Camilo Valencia Estrada zeigt eine analytische Lösung des Problems für bestimmte Einzelfälle.[10]
- Rafael G. González-Acuña und Héctor A. Chaparro-Romo präsentieren die allgemeine Gleichung der geschlossenen Form für den Entwurf einer Linse ohne sphärische Aberration.[11][12][13][14][15][16][17]
Referenzen
- Applied Optics Volume 57, Issue 31. In: www.osapublishing.org. OSA Publishing. November 2018. Abgerufen am 29. April 2019.
- Toomer G. J.: Diocles On Burning Mirrors, Sources in the History of Mathematics and the Physical Sciences 1. Springer, New York 1976.
- R. Rashed: Géométrie et dioptrique au Xe siècle: Ibn Sahl, al-Quhi et Ibn al-Haytham.. Les Belles Lettres, Paris 1993.
- Christiaan Huygens: Traité de la lumière 1690.
- Fokko Jan Dijksterhuis: Lenses and waves: Christiaan Huygens and the mathematical science of optics in the seventeenth century. Springer, Enschede 2004, ISBN 978-1-4020-2697-3.
- T. Levi-Civita: Complementi al teorema di Malus-Dupin. Nota I. In: Atti Accad. Sci. Torino. 9, Nr. 5, Januar, S. 185–189.
- G. D. Wasserman, E. Wolf: On the Theory of Aplanatic Aspheric Systems. In: Proceedings of the Physical Society. 62, Nr. 1, Januar.
- Daniel Malacara: Two Lenses to Collimate Red Laser Light. In: Applied Optics. 4, Nr. 12, Januar, S. 1652–1654. doi:10.1364/AO.4.001652.
- Psang Dain Lin, Chung-Yu Tsai: Determination of unit normal vectors of aspherical surfaces given unit directional vectors of incoming and outgoing rays. In: Applied Optics. 29, Nr. 2, Januar, S. 174–178. doi:10.1364/JOSAA.29.000174.
- Juan Camilo Valencia-Estrada, Ricardo Benjamín. Flores-Hernández: Singlet lenses free of all orders of spherical aberration. In: Royal Society proceedings A. 471, Januar. doi:10.1098/rspa.2014.0608.
- Rafael G. González-Acuña, Héctor A. Chaparro-Romo: General formula for bi-aspheric singlet lens design free of spherical aberration. In: Applied Optics. 57, Nr. 31, Januar, S. 9341–9345. doi:10.1364/AO.57.009341.
- Rafael G. González-Acuña, Gutiérrez-Vega Julio C.: Generalization of the axicon shape: the gaxicon. In: Journal of the Optical Society of America A. 35, Nr. 11, Januar, S. 1915–1918. doi:10.1364/JOSAA.35.001915.
- Danilo Moreno: Nuevos lentes se diseñan en laboratorios de Yachay Tech. In: www.elnorte.ec. Diario El Norte. 1. Januar 2019. Abgerufen am 29. April 2019.
- Julio Chacón, docente YACHAY TECH, Proyecto de Investigación de Lentes libres de aberraciones esféricas.. In: www.elnorte.ec. Diario El Norte. 6. Dezember 2018. Abgerufen am 29. April 2019.
- YACHAY TECH CONTRIBUYE AL DISEÑO DE NUEVOS LENTES. In: https://www.yachaytech.edu.ec. YachayTech. 3. Dezember 2018. Abgerufen am 29. April 2019.
- ¡Eureka! Encuentran la fórmula para resolver un antiguo problema óptico. In: https://transferencia.tec.mx. Revista Transferencia Tec. 21. Februar 2019. Abgerufen am 29. April 2019.
- Rafael G. González-Acuña, Maximino Avendaño-Alejo, Gutiérrez-Vega Julio C.: Singlet lens for generating aberration-free patterns on deformed surfaces. In: Journal of the Optical Society of America A. 36, Nr. 5, Januar, S. 925–929. doi:10.1364/JOSAA.36.000925.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.