Kristalloptik

Die Kristalloptik beschäftigt sich mit der Wechselwirkung elektromagnetischer Strahlung, in der Regel im sichtbaren Wellenlängenbereich, mit kristallinen oder anderweitig anisotropen Festkörpern, aber verallgemeinernd auch mit optisch aktiven Flüssigkeiten. Sie ist ein Teilgebiet der Optik, der Festkörperphysik und der Mineralogie.

Hintergrund

Die optischen Eigenschaften von Kristallen, die u. a. für Reflexion, Refraktion und Absorption des Lichtes verantwortlich sind, sind durch ihren regelmäßigen inneren Aufbau bestimmt. Anders als bei den optisch isotropen Gläsern findet man bei Kristallen in der Regel das Phänomen der Anisotropie: Wichtige Eigenschaften wie z. B. der Brechungsindex sind von der Ausbreitungsrichtung des Lichts im Kristall und seiner Polarisation abhängig (genauer gesagt gilt dies für alle Kristalle, die nicht das kubische Kristallsystem aufweisen).

Zur Veranschaulichung trägt man in einem dreidimensionalen Diagramm für jede mögliche Wellennormalenrichtung von Licht im Kristall den Wert der Brechungsindizes in den beiden Schwingungsrichtungen senkrecht zu dieser Richtung ein. Dadurch ergibt sich immer ein Ellipsoid mit im Allgemeinen drei ungleichen senkrecht aufeinander stehenden Hauptachsen, das man auch als Indexellipsoid, Fletcher-Ellipsoid oder Indikatrix bezeichnet:

Ist der Kristall kubisch, dann reduziert sich das Ellipsoid auf den Spezialfall einer Kugel, da alle drei Hauptachsen dieselbe Länge haben. Die Lichtausbreitung ist in diesem Falle isotrop.

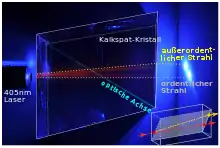
Doppelbrechung an einem Kalkspat-Kristall:
ordentlicher und außerordentlicher Strahl sind durch rote Fluoreszenz im Kristall sichtbar

Im Falle des hexagonalen, trigonalen und tetragonalen Kristallsystems sind nur zwei der Hauptachsen gleich lang (Rotationsellipsoid), man spricht dann von optisch einachsigen oder uniaxialen Kristallen. Die in der Bezeichnung angesprochene optische Achse steht senkrecht auf den beiden gleich langen Hauptachsen. Nur bei Lichteinfall parallel zu dieser Achse findet keine Doppelbrechung statt.
Drei unterschiedlich lange Hauptachsen (dreiachsiges Ellipsoid) finden sich für das orthorhombische, monokline und trikline Kristallsystem, der Kristall heißt nun optisch zweiachsig oder biaxial. Diese beiden Achsen fallen nicht mit Hauptachsen des Ellipsoids zusammen; vielmehr sind sie eindeutig dadurch definiert, dass sie senkrecht auf den beiden einzigen Kreisen stehen, die sich durch den Schnitt einer Ebene mit dem Ellipsoid durch seinen Mittelpunkt erzeugen lassen (alle anderen Schnitte ergeben keine Kreise, sondern Ellipsen). Der Radius dieser Kreise entspricht der von der Länge her mittleren der drei Hauptachsen.

Eine wichtige Folge der Anisotropie von Kristallen ist die Doppelbrechung, d. h. die Aufspaltung von Licht, das auf den Kristall trifft, in einen ordentlichen und einen außerordentlichen Strahl, die eine unterschiedliche Polarisation aufweisen.

Auch die optische Aktivität von Kristallen lässt sich auf ihre Anisotropie zurückführen: Dabei wird die Polarisationsebene linear polarisierten Lichtes um einen Winkel gedreht, der proportional ist zur im Kristall zurückgelegten Strecke. Je nachdem ob die Ebene im Uhrzeiger- oder im Gegenuhrzeigersinn gedreht wird, wenn man genau gegen die Ausbreitungsrichtung des Lichtes schaut, unterscheidet man rechts- und linksdrehende Kristalle, die auch als optische Modifikationen bezeichnet werden. Beispiele sind Links- und Rechtsquarz.

Eine dritte spezifisch auf Kristalle zutreffende optische Erscheinung ist der Pleochroismus. Das bedeutet, dass Licht je nach Ausbreitungs- und Polarisationsrichtung unterschiedlich stark absorbiert wird. Da die Absorption zusätzlich noch von der Wellenlänge abhängt, zeigt sich der Pleochronismus in einer richtungsabhängigen Farbänderung des durchstrahlten Lichtes, die in extremen Fällen schon mit bloßem Auge feststellbar ist.

Die optischen Eigenschaften eines Kristalls lassen sich durch äußere elektrische und magnetische Felder beeinflussen, aber auch durch mechanische Belastung. Im ersten Fall spricht man vom elektrooptischen Effekt, im zweiten vom magnetooptischen Effekt. Umgekehrt können diese Effekte zur Diagnose der externen Einflüsse herangezogen werden.

Mathematischer Formalismus

Grundlage des mathematischen Formalismus ist die Tatsache, dass die elektrische Feldstärke ${\vec {E}}$ und die elektrische Verschiebungsdichte ${\vec {D}}$ nicht mehr gleich gerichtet sind. Damit kann die dielektrische Funktion $\varepsilon$ , welche die beiden Formelgrößen verknüpft, nicht mehr als Skalar aufgefasst werden, sondern muss als Tensor zweiter Stufe behandelt werden. Die Beziehung zwischen ${\vec {D}}$ und ${\vec {E}}$ schreibt sich nun:

${\begin{pmatrix}D_{x}\\D_{y}\\D_{z}\end{pmatrix}}=\varepsilon _{0}{\begin{pmatrix}\varepsilon _{xx}&\varepsilon _{xy}&\varepsilon _{xz}\\\varepsilon _{yx}&\varepsilon _{yy}&\varepsilon _{yz}\\\varepsilon _{zx}&\varepsilon _{zy}&\varepsilon _{zz}\end{pmatrix}}\cdot {\begin{pmatrix}E_{x}\\E_{y}\\E_{z}\end{pmatrix}},$

wobei $\varepsilon _{0}$ die Dielektrizitätskonstante des Vakuums darstellt.

Wie sich eine elektromagnetische Welle im anisotropen Medium ausbreitet, lässt sich durch Lösen der Wellengleichung für anisotrope Körper berechnen:

\varepsilon \cdot {\vec {E}}=n^{2}({\vec {E}}-{\vec {k}}({\vec {E}}\cdot {\vec {k}}))

.

Hier stellt ${\vec {k}}$ einen Einheitsvektor dar, der in Ausbreitungsrichtung der Welle zeigt, n ist der Brechungsindex.

Algebraisch ist die Wellengleichung ein System aus drei gekoppelten Gleichungen, aus dem sich die zwei Brechungsindizes für die beiden verschiedenen Polarisationsrichtungen ableiten lassen. Das Gleichungssystem ist jedoch im Allgemeinen in Bezug auf die Polarisationsrichtung nicht eindeutig. Deshalb wird ein Verfahren benutzt, um die drei Gleichungen auf zwei zu reduzieren. Zunächst konstruiert man ein System aus drei paarweise senkrecht aufeinander stehenden Vektoren. Zwei davon sind die Ausbreitungsrichtung ${\vec {k}}$ und Verschiebungsdichte ${\vec {D}}$ , der dritte ist die magnetische Feldstärke ${\vec {H}}$ . Da ${\vec {k}}$ nicht mehr wie im isotropen Festkörper im 90-Grad-Winkel zu ${\vec {E}}$ stehen muss, ist die Wellengleichung nicht geeignet, um den Polarisierungscharakter der Wellen zu bestimmen.

Nun wird ausgenutzt, dass ${\vec {D}}$ senkrecht auf der Ausbreitungsrichtung ${\vec {k}}$ steht. Es ist

{\vec {E}}=(\varepsilon )^{-1}\cdot {\vec {D}}

,

wobei $(\varepsilon )^{-1}$ der zu $(\varepsilon )$ inverse Tensor ist. Durch Wahl eines neuen Koordinatensystems mit den Koordinaten a, b, c, das so gewählt ist, dass die c-Richtung parallel zu ${\vec {k}}$ liegt, kann man das Gleichungssystem von drei auf zwei Gleichungen reduzieren:

D_{a}=n^{2}\varepsilon _{aa}^{-1}D_{a}+n^{2}\varepsilon _{ab}^{-1}D_{b}

D_{b}=n^{2}\varepsilon _{ba}^{-1}D_{a}+n^{2}\varepsilon _{bb}^{-1}D_{b}

Durch Lösen dieses Gleichungssystems erhält man die beiden Brechungsindizes und den Polarisationscharakter für jede beliebige Richtung.

Literatur

Werner Döring: Einführung in die Theoretische Physik, Band III (Optik). Sammlung Göschen, Berlin 1957.

Weblinks

H.-G. Stosch: Skript zur Kristalloptik II – Mineralmikroskopie. (PDF 21789 kB) In: agw.kit.edu. Uni Freiburg, 14. Oktober 2009, abgerufen am 23. September 2019.
Interferenzfiguren an doppelbrechenden, optisch aktiven Kristallplättchen

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.