Beugung (Physik)
Die Beugung oder Diffraktion ist die Ablenkung von Wellen an einem Hindernis. Durch Beugung kann sich eine Welle in Raumbereiche ausbreiten, die auf geradem Weg durch das Hindernis versperrt wären. Jede Art von physikalischen Wellen kann Beugung zeigen. Besonders deutlich erkennbar ist sie bei Wasserwellen oder bei Schall. Bei Licht ist die Beugung ein Faktor, der das Auflösungsvermögen von Kamera-Objektiven und Teleskopen begrenzt. Manche technische Komponenten, wie Beugungsgitter, nutzen die Beugung gezielt aus.
Zur Beugung kommt es durch Entstehung neuer Wellen entlang einer Wellenfront gemäß dem huygens-fresnelschen Prinzip. Diese können durch Überlagerung zu Interferenzerscheinungen führen.
Im Gegensatz zur Beugung findet bei der Streuung eine Ablenkung von Strahlung durch Interaktion von Teilchen statt. Bei gleichgerichteter, kohärenter Streuung spricht man auch von Reflexion.
Bei der Brechung beruht die Ablenkung einer Strahlung auf der Änderung der Ausbreitungsgeschwindigkeit bei Änderung der Dichte oder der Zusammensetzung des Ausbreitungsmediums, am deutlichsten beim Durchtritt durch eine Phasengrenze.
Geschichte
Christiaan Huygens bemerkte bereits um 1650, dass mit einer Lichtausbreitung in Wellenform bestimmte bis dahin unerklärliche Phänomene beschrieben werden können. Er formulierte das Huygenssche Prinzip und begründete damit die Wellenoptik. Der Effekt der Beugung von Licht an einem optischen Spalt wurde schließlich 1662 von Francesco Maria Grimaldi beobachtet, der das Licht in seinem Werk De lumine als Welle beschrieb. 1802 führte Thomas Young entsprechende Experimente am Doppelspalt durch. Eine vollständige physikalische Beschreibung der Beugung konnte 1818 durch Augustin Jean Fresnel erbracht werden, die von Siméon Denis Poisson zunächst in Zweifel gezogen wurde, kurz darauf jedoch von François Arago durch den experimentellen Nachweis der von Poisson selbst theoretisch vorhergesagten Poisson-Flecken bei der Beugung an einer Kugel bestätigt werden konnte.
1835 untersuchte Friedrich Magnus Schwerd Beugungserscheinungen an regelmäßigen Gittern, die mit Hilfe der Wellenoptik ebenfalls beschrieben werden konnten. 1909 konnte Geoffrey Ingram Taylor im Taylor-Experiment zeigen, dass auch Licht mit äußerst geringer Intensität, also auch einzelne Photonen gebeugt werden, womit der Welle-Teilchen-Dualismus nachgewiesen werden konnte.
1924 entwickelte Louis-Victor de Broglie die Theorie der Materiewellen, und bereits drei Jahre später konnten Clinton Joseph Davisson und George Paget Thomson durch Versuche zur Elektronenbeugung zeigen, dass auch Teilchen mit Masse gebeugt werden. Weitere drei Jahre später konnten Otto Stern, Otto Robert Frisch und Immanuel Estermann diesen Effekt auch bei der Beugung von Strahlen aus Heliumatomen und Wasserstoffmolekülen an einem Lithiumfluoridkristall demonstrieren. Claus Jönsson führte 1961 schließlich auch Experimente zur Beugung von Elektronen an Einzel- und Doppelspalten aus.
Beugung an Blenden
Wegen der Wellennatur des Lichtes weicht sein reales Verhalten teilweise stark von jenem ab, was die geometrische Optik erwarten ließe. So ist bei der Fotografie beugungsbedingt die Auflösung eines Fotos durch den Durchmesser (Apertur) der Linse begrenzt.
Das physikalische Modell für Beugung ist das huygens-fresnelsche Prinzip. Zur Berechnung von Beugungsbildern wird das kirchhoffsche Beugungsintegral verwendet, dessen zwei Grenzfälle die Fresnel-Beugung (divergierende Punktstrahlungsquelle) und die Fraunhofer-Beugung sind (parallele Lichtstrahlen als Strahlungsquelle).[2] Die Überlagerung der Elementarwellen kann zu gegenseitiger Verstärkung (konstruktive Interferenz) oder gegenseitiger Abschwächung (destruktive Interferenz) oder gar Auslöschung führen, siehe auch bei Gangunterschied.
Beugung kann unter anderem gut beobachtet werden, wenn geometrische Strukturen eine Rolle spielen, deren Größe mit der Wellenlänge der verwendeten Wellen vergleichbar ist. Optische Blenden werden je nach Anwendung so dimensioniert, dass sie Beugungseffekte bewirken – also bei Abmessungen im Bereich und unterhalb der Lichtwellenlänge, oder mit hinreichender Genauigkeit keine – dann mit Abmessungen deutlich über der Lichtwellenlänge.
Beispiele für Beugung an Blenden
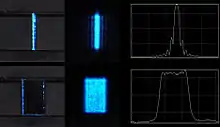
Beugung am Einfachspalt: Teilt man in Gedanken ein Lichtbündel, das an einem Einfachspalt in eine bestimmte Richtung abgelenkt wird, in zwei Hälften, können sich diese beiden Anteile des Lichtbündels konstruktiv oder destruktiv überlagern. An einem Spalt ergibt sich so wieder eine Reihe von Beugungsmaxima.
Wenn die Schlitzbreite deutlich kleiner ist als die Wellenlänge, entstehen dahinter Zylinderwellen.
Beugung am Einfachspalt
Beugung am Einfachspalt – Licht längerer Wellenlänge (grün) wird stärker gebeugt, das Beugungsbild ist weiter aufgefächert
Beugung am Einfachspalt – Licht kürzerer Wellenlänge (blau) wird bei gleicher Spaltbreite weniger stark gebeugt, das Beugungsbild ist enger
Beugung des Lichts der Sonne an einer kreisförmigen Lochblende - je kürzer die Wellenlänge, desto geringer werden die entsprechenden Farbanteile gebeugt
An Blenden anderer Form ergeben sich teilweise stark abweichende Beugungsmuster.
Beugung an einer kreisförmigen Öffnung
Beugung an einer rechteckigen Öffnung
Beugung am Gitter
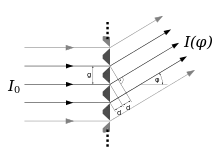
Gitter sind Blenden mit periodischen Spalten. Die Beugung am Gitter ist damit ein wichtiger Spezialfall der Beugung an Blenden.
- Optisches Gitter
- Sind in regelmäßigen Abständen viele Spalte angeordnet, ergibt sich eine Reihe von Beugungsreflexen, deren Anordnung derjenigen entspricht, die man bei einem Doppelspalt mit dem gleichen Abstand erwartet. Mit zunehmender Anzahl der Einzelspalten werden die Reflexe aber zu immer schärferen Linien. Da die Lage der Reflexe von der Wellenlänge des Lichtes abhängt, kann man optische Gitter zur Trennung verschiedener Wellenlängen nutzen. Das ist im Monochromator und bei der Spektroskopie der Fall. In der Praxis werden sehr häufig regelmäßige Anordnungen von spiegelnden und nicht spiegelnden Streifen als Reflexionsgitter verwendet. Die nicht bedruckte Seite einer CD wirkt ähnlich.
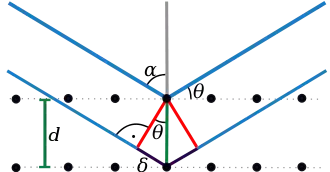
- Röntgenbeugung
- Diese wird in der Kristallographie zum Bestimmen und Vermessen von Kristallgittern verwendet. Die Wellenlänge der Röntgenstrahlung ist mit den Gitterabständen im Kristall vergleichbar, und das Kristallgitter wirkt als mehrdimensionales optisches Gitter.
Weitere Wellenarten
Prinzipiell gelten Gesetzmäßigkeiten, die für die Beugung von Lichtwellen gelten, auch für andere Wellenerscheinungen.
- In der Akustik: Die Beugung von Schall ist für die Berechnung der abschirmenden Wirkung von Lärmschutzwänden wichtig.
- In der Teilchenphysik beschäftigt man sich unter anderem mit der Elektronenbeugung.
- Beim Richtfunk spielt die Beugung an Hindernissen im Ausbreitungsweg für die Dämpfung oder Verstärkung des Signals eine Rolle, siehe Fresnelzone.
- Wasserwellen: Im Wasser gibt es interessante Überlagerungen von Wellen (Kaimauern, Motorboote usw.), und es können sich durch Überlagerungseffekte Monsterwellen ausbilden. Ähnliche Effekte kann man zur Ortung von U-Booten, Fischschwärmen u. a. unter Wasser verwenden.
- In der Quantenmechanik hat jedes Teilchen prinzipiell auch Welleneigenschaften, somit ist eine Beugung von Teilchenstrahlen möglich, wenn auch experimentell schwer zugänglich. Es konnte z. B. die Beugung von Strahlen aus C60-Molekülen im Experiment nachgewiesen werden.[3]
- Beugung von Heliumatomen als Untersuchungsmethode in der Oberflächenphysik (Heliumatomstrahlstreuung).
Weblinks
Einzelnachweise und Kommentare
- F. Dorn, F. Bader: Physik-Oberstufe. Schroedel, Hannover 1986, ISBN 3-507-86205-0.
- Sowohl bei der Fresnel’schen Beugung als auch bei der Fraunhofer’schen Beugung handelt es sich bzgl. der Maxwell’schen Gleichungen um Fernfeldnäherungen, weil der Abstand der Beugungsobjekte von der Lichtquelle in beiden Fällen i. a. sehr viel größer ist als die Lichtwellenlänge.
- Markus Arndt, Olaf Nairz, Julian Vos-Andreae, Claudia Keller, Gerbrand van der Zouw, Anton Zeilinger: Wave-particle duality of C60 molecules. In: Nature. Band 401, Nr. 6754, 14. September 1999, S. 680–682, doi:10.1038/44348.