Abbildungsmaßstab

Der Abbildungsmaßstab (Formelzeichen $\beta$ [1]), kurz oft Maßstab genannt, ist definiert als das Verhältnis zwischen der Bildgröße $y'$ der optischen Abbildung eines Gegenstandes und dessen realer Objektgröße $y$ oder Dinggröße. Alternativ kann der Abbildungsmaßstab auch über das Verhältnis von Bildweite $a'$ zur Objektweite $a$ bestimmt werden:

\beta ={\frac {y'}{y}}={\frac {a'}{a}}

[1][2]

Für $y=1$ oder für $y'=1$ ist es oft üblich, den Betrag des Abbildungsmaßstabs als das Verhältnis 1:y beziehungsweise y':1 anzugeben. Ist der Abbildungsmaßstab größer als 1 (in der Reproduktionstechnik meist als 100 % angegeben[3]) spricht man von Vergrößerung, bei $\beta <1$ von Verkleinerung.

Ein Abbildungsmaßstab mit dem Betrag 1 (bzw. 100 %) sagt aus, dass der Gegenstand und seine Abbildung gleich groß sind.
Ein Abbildungsmaßstab mit dem Betrag 0,5 (bzw. 50 %) sagt aus, dass der Gegenstand doppelt so groß ist wie seine Abbildung.
Ein Abbildungsmaßstab mit dem Betrag 2 (bzw. 200 %) sagt aus, dass die Abbildung doppelt so groß ist wie der Gegenstand.

Fotografie

In der Fotografie bezeichnet man als Abbildungsmaßstab den Betrag des Verhältnisses der Abbildungsgröße eines Objektes auf der Bildebene zur Größe des Originalobjektes selbst. Der Abbildungsmaßstab nimmt mit kleiner werdendem Abstand zum Objekt und mit Verlängerung der Objektivbrennweite zu.

Aufgrund der einem jeden Objektiv eigenen Naheinstellgrenze (der Mindestabstand zum Objekt), unterhalb derer es nicht mehr möglich ist, auf das Objekt zu fokussieren, kann der Objektabstand allerdings nicht beliebig verringert werden.

Spezielle Objektive für die Makrofotografie, die sogenannten Makro-Objektive, können mit einem besonders geringen Objektabstand eingesetzt werden und ermöglichen dadurch einen besonders großen Abbildungsmaßstab, wie beispielsweise 0,5 (die Abbildung ist halb so groß wie das Objekt) oder 1 (Objekt wird in Originalgröße in der Bildebene abgebildet). Bei einem Abbildungsmaßstab von mindestens 0,25 wird ein Objektiv als makrofähig bezeichnet. Normale Objektive erzielen maximale Abbildungsmaßstäbe im Bereich von 1:7 bis 1:9.

Ein Anfang der 1990er Jahre vorgestelltes Spezialobjektiv von Minolta, das Minolta AF Macro Zoom 3x–1x (1:1,7–1:2,8), ermöglicht sogar einen Abbildungsmaßstab von 3; es kann also ein Objekt dreifach vergrößert in die Bildebene abbilden. Um derartige Abbildungsmaßstäbe ohne Spezialobjektive zu erzielen, müssen normalerweise ein Balgengerät, Zwischenringe und zusätzlich ein Objektiv in Retrostellung zur Vermeidung von Farbfehlern eingesetzt werden.

Beispiele zur Berechnung des Abbildungsmaßstabes:

Bildet die Kamera einen 20 cm hohen Kopf in der Bildebene mit einer Höhe von 0,5 Zentimetern ab, so ist der Betrag des Abbildungsmaßstabs 0,5:20 = 1:40 = 0,025
Wird ein 36 Millimeter langes Insekt in der Bildbreite von 36 Millimetern formatfüllend auf Kleinbildfilm abgebildet, bedeutet dies, dass der Abbildungsmaßstab 1 beträgt

Häufig unterlassen es die Hersteller von Wechselobjektiven, den mit einem bestimmten Objektiv erzielbaren Abbildungsmaßstab anzugeben; stattdessen wird häufig nur der kürzestmögliche Objektabstand angegeben. Diese Angabe lässt jedoch nur einen indirekten Rückschluss über den effektiv erzielbaren Abbildungsmaßstab zu, zumal viele Objektive mit Kameragehäusen verschiedener Bildsensorgrößen verwendet werden können. Mit Testaufnahmen lässt sich der Abbildungsmaßstab jedoch ermitteln.

Räumliche Motive

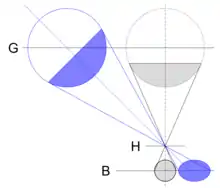
Verzerrung bei der optischen Abbildung einer Kugel in der Gegenstandsebene G über die Hauptebene H in die Bildebene B.

Kugelförmiges Leuchtmittel aus sehr kurzem Abstand mit einem verzeichnungsfreien Ultraweitwinkelobjektiv aufgenommen. Der rechte Rand der Abbildung der Kugel ist in der Bildmitte, der linke Rand der Kugel ist am linken Bildrand. Es ist wegen des Bildseitenverhältnisses von 2:1 deutlich zu erkennen, dass die Breite der abgebildeten Kugel deutlich größer ist als die Höhe, so dass deren Rand ellipsenförmig erscheint.

Bei der Abbildung von räumlichen Objekten variiert der Abbildungsmaßstab mit der Objektweite. Die daraus resultierenden geometrischen Effekte sind keine Abbildungsfehler der verwendeten Objektive.[4]

Dies kann zum Beispiel dazu führen, dass parallele Objektkanten als nicht-parallele stürzende Linien abgebildet werden.

Die Strahlen vom kreisförmigen Rand einer Kugel, deren Mittelpunkt sich nicht auf der optischen Achse befindet, werden bei einer optischen Abbildung zwangsläufig bei unterschiedlichen Objektweiten erfasst und haben in der Abbildung daher verschiedene Abbildungsmaßstäbe, die zu einer geometrischen Verzerrung der Kreisform in der Abbildung führen. Die näher an der optischen Achse liegenden Objektpunkte liegen weiter entfernt als die Objektpunkte, die weiter von der optischen Achse entfernt sind. Deswegen ist der Abbildungsmaßstab umso größer, je weiter sich die Bildpunkte am Bildrand befinden. Insbesondere bei der Verwendung von Weitwinkelobjektiven kann dies wegen der großen Bildwinkel zu deutlich erkennbaren Deformationen in den Abbildungen führen.

Relativer Abbildungsmaßstab

Der relative Abbildungsmaßstab $m_{\text{rel}}$ ist definiert als das Verhältnis des Maßstabs $m$ einer optischen Abbildung mit der Brennweite $f$ zum Maßstab $m_{\mathrm {N} }$ bei einer optischen Abbildung mit der Normalbrennweite $f_{\mathrm {N} }$ :

m_{\text{rel}}={\frac {m}{m_{\mathrm {N} }}}

Gleichzeitig ist für große Entfernungen der abgebildeten Gegenstände (die Gegenstandsweite ist deutlich größer als die Brennweite $f$ ) der relative Abbildungsmaßstab näherungsweise auch durch folgenden Ausdruck gegeben:

m_{\text{rel}}={\frac {f}{f_{\mathrm {N} }}}

Siehe auch

Literatur

Gottfried Schröder: Technische Fotografie: Grundlagen und Anwendungen in Technik und Wissenschaft, Vogel-Druck, Würzburg, 1. Auflage, 1981

Weblinks

Wiktionary: Abbildungsmaßstab – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Abbildungsmaßstab, Wikibook Digitale bildgebende Verfahren (2013)

Einzelnachweise

Siehe DIN 4522-7:1991-04 und DIN 1335:2003-12
Helmut Naumann, Gottfried Schröder, Martin Löffler-Mang: Handbuch Bauelemente der Optik: Grundlagen, Werkstoffe, Geräte, Messtechnik, Carl Hanser Verlag, 2014, ISBN 9783446441156
Hans F. Ebel, Claus Bliefert: Vortragen in Naturwissenschaft, Technik und Medizin. 1991; 2., bearbeitete Auflage 1994; 3. Auflage, Wiley-VCH, Weinheim 2005, ISBN 3-527-31225-0, S. 293.
Räumliche Motive, in: Digitale bildgebende Verfahren - Bildaufnahme, abgerufen am 26. Oktober 2018

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[DIN-1] Siehe DIN 4522-7:1991-04 und DIN 1335:2003-12

[2] Helmut Naumann, Gottfried Schröder, Martin Löffler-Mang: Handbuch Bauelemente der Optik: Grundlagen, Werkstoffe, Geräte, Messtechnik, Carl Hanser Verlag, 2014, ISBN 9783446441156

[3] Hans F. Ebel, Claus Bliefert: Vortragen in Naturwissenschaft, Technik und Medizin. 1991; 2., bearbeitete Auflage 1994; 3. Auflage, Wiley-VCH, Weinheim 2005, ISBN 3-527-31225-0, S. 293.

[4] Räumliche Motive, in: Digitale bildgebende Verfahren - Bildaufnahme, abgerufen am 26. Oktober 2018